题目内容
已知:在平面直角坐标系中,等腰直角△ABC顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,-2),C(1,0),点B在第四象限时,先写出点B的坐标,并说明理由.
(2)如图2,当点C在x轴正半轴上运动,点A(0,a)在y轴正半轴上运动,点B(m,n)在第四象限时,作BD⊥y轴于点D,试判断a,m,n之间的关系,请证明你的结论.
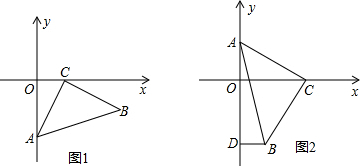
(1)如图1,当A(0,-2),C(1,0),点B在第四象限时,先写出点B的坐标,并说明理由.
(2)如图2,当点C在x轴正半轴上运动,点A(0,a)在y轴正半轴上运动,点B(m,n)在第四象限时,作BD⊥y轴于点D,试判断a,m,n之间的关系,请证明你的结论.
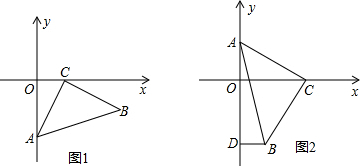
分析:(1)过点B作BD⊥x轴于D,利用同角的余角相等求出∠OAC=∠BCD,然后利用“角角边”证明△AOC和△CDB全等,根据全等三角形对应边相等可得AO=CD,OC=BD,然后求出OD,再根据点D在第四象限写出点D的坐标即可;
(2)过点B作BE⊥x轴于E,利用同角的余角相等求出∠2=∠3,再利用“角角边”证明△CEB和△AOC全等,根据全等三角形对应边相等可得AO=CE,BE=CO,然后代入a、m、n整理即可得解.
(2)过点B作BE⊥x轴于E,利用同角的余角相等求出∠2=∠3,再利用“角角边”证明△CEB和△AOC全等,根据全等三角形对应边相等可得AO=CE,BE=CO,然后代入a、m、n整理即可得解.
解答:解:(1)点B的坐标为(3,-1).
理由如下:作BD⊥x轴于D,
∴∠BOC=90°=∠BDC,
∴∠OAC+∠ACO=90°,
∵∠ACB=90°,AC=BC,
∴∠ACO+∠BCD=90°,
∴∠OAC=∠BCD,
在△AOC和△CDB中,
,
∴△AOC≌△CDB(AAS),
∴AO=CD,OC=BD,
∵A(0,-2),C(1,0),
∴AO=CD=2,OC=BD=1,
∴0D=3,
∵B在第四象限,
∴点B的坐标为(3,-1);
(2)a+m+n=0.
证明:作BE⊥x轴于E,
∴∠BEC=∠AOC=90°,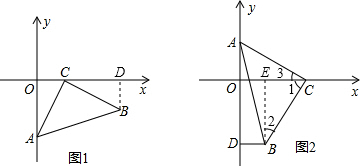
∴∠1+∠2=90°,
∵∠ACB=90°,
∴∠1+∠3=90°,
∴∠2=∠3,
在△CEB和△AOC中,
,
∴△CEB≌△AOC(AAS),
∴AO=CE=a,BE=CO,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴EO=BD=m,
∴BE=-n,
∴a+m=-n,
∴a+m+n=0.
理由如下:作BD⊥x轴于D,
∴∠BOC=90°=∠BDC,
∴∠OAC+∠ACO=90°,
∵∠ACB=90°,AC=BC,
∴∠ACO+∠BCD=90°,
∴∠OAC=∠BCD,
在△AOC和△CDB中,
|
∴△AOC≌△CDB(AAS),
∴AO=CD,OC=BD,
∵A(0,-2),C(1,0),
∴AO=CD=2,OC=BD=1,
∴0D=3,
∵B在第四象限,
∴点B的坐标为(3,-1);
(2)a+m+n=0.
证明:作BE⊥x轴于E,
∴∠BEC=∠AOC=90°,
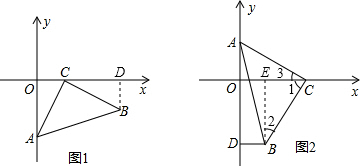
∴∠1+∠2=90°,
∵∠ACB=90°,
∴∠1+∠3=90°,
∴∠2=∠3,
在△CEB和△AOC中,
|
∴△CEB≌△AOC(AAS),
∴AO=CE=a,BE=CO,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴EO=BD=m,
∴BE=-n,
∴a+m=-n,
∴a+m+n=0.
点评:本题考查了全等三角形的判定与性质,坐标与图形的性质,等腰直角三角形的性质,同角的余角相等的性质,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目

 如图,在平面直角坐标中,已知直线y=kx+b与直线
如图,在平面直角坐标中,已知直线y=kx+b与直线 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数