题目内容
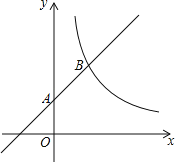
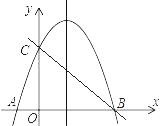
【题目】如图，抛物线y＝﹣x2+3x+4交x轴于A、B两点（点A在B左边），交y轴于点C．
（1）求A、B两点的坐标；
（2）求直线BC的函数关系式；
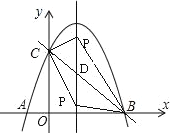
（3）点P在抛物线的对称轴上，连接PB，PC，若△PBC的面积为4，求点P的坐标．
【答案】（1）A、B两点坐标为（-1，0）和（4，0），（2）y=-x+4，（3）点P的坐标为（
，
）或（，
）
【解析】
试题（1）令y=0得﹣x2+3x+4=0解得方程的解即为A、B两点坐标；（2）令x=0，解得抛物线y=﹣x2+3x+4与y轴交点C的坐标，设直线BC的函数关系式y=kx+b，解得k和b的值即可得出直线BC的函数关系式； （3）求得抛物线y=﹣x2+3x+4的对称轴，设对称轴与直线BC的交点记为D，求得D点坐标，设点P的坐标，表示出PD，再根据三角形的面积公式得出点P的坐标．
试题解析：
（1）由﹣x2+3x+4=0解得x=﹣1或x=4，
所以A、B两点坐标为（﹣1，0）和（4，0）；
（2）抛物线y=﹣x2+3x+4与y轴交点C坐标为（0，4），由（1）得，B（4，0），
设直线BC的函数关系式y=kx+b，
∴
，
解得
，
∴直线BC的函数关系式为y=﹣x+4；
（3）抛物线y=﹣x2+3x+4的对称轴为x=，
对称轴与直线BC的交点记为D，则D点坐标为（，
）．
∵点P在抛物线的对称轴上，
∴设点P的坐标为（，m），
∴PD=|m﹣|，
∴S△PBC=OBPD=4．
∴×4×|m﹣|=4，
∴m=或m=．
∴点P的坐标为（，
）或（，）．
状元及第系列答案
同步奥数系列答案【题目】从共享单车，共享汽车等共享出行到共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速的普及，根据国家信息中心发布的中国分享经济发展报告2017显示，参与共享经济活动超6 亿人，比上一年增加约1亿人．
（1）为获得北京市市民参与共享经济活动信息，下列调查方式中比较合理的是 ；
A．对某学校的全体同学进行问卷调查
B．对某小区的住户进行问卷调查
C．在全市里的不同区县，选取部分市民进行问卷调查
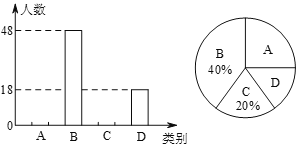
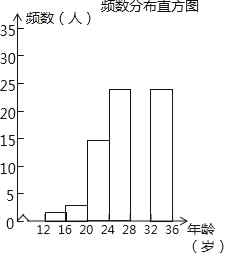
（2）调查小组随机调查了延庆区市民骑共享单车情况，某社区年龄在12～36岁的人有1000人，从中随机抽取了100人，统计了他们骑共享单车的人数，并绘制了如下不完整的统计图表．如图所示．骑共享单车的人数统计表
年龄段（岁） | 频数 | 频率 |
12≤x＜16 | 2 | 0.02 |
16≤x＜20 | 3 | 0.03 |
20≤x＜24 | 15 | a |
24≤x＜28 | 25 | 0.25 |
28≤x＜32 | b | 0.30 |
32≤x＜36 | 25 | 0.25 |
根据以上信息解答下列问题：
①统计表中的a＝ ；b＝ ；
②补全频数分布直方图；
③试估计这个社区年龄在20岁到32岁（含20岁，不含32岁）骑共享单车的人有多少人？
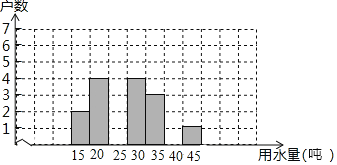
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况：：
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
（1）求出m＝ ，补充画出这20户家庭三月份用电量的条形统计图；
（2）据上表中有关信息，计算或找出下表中的统计量，并将结果填入表中：
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
（3）为了倡导“节约用水绿色环保”的意识，江赣市自来水公司实行“梯级用水、分类计费”，价格表如下：
月用水梯级标准 | Ⅰ级（30吨以内） | Ⅱ级（超过30吨的部分） |
单价（元/吨） | 2.4 | 4 |
如果该小区有500户家庭，根据以上数据，请估算该小区三月份有多少户家庭在Ⅰ级标准？
（4）按上表收费，如果某用户本月交水费120元，请问该用户本月用水多少吨？
