题目内容
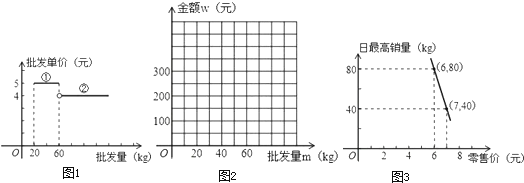
【题目】已知某种水果的批发单价与批发量的函数关系如图1所示.
(1)请说明图中①、②两段函数图象的实际意义;
(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在图2的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果;
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图3所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.
【答案】(1)详见解析;(2)详见解析;(3)经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获得最大利润160元.
【解析】
(1)(2)中要注意变量的不同的取值范围;
(3)可根据图中给出的信息,用待定系数的方法来确定函数.然后根据函数的特点来判断所要求的值.
解:(1)图①表示批发量不少于20kg且不多于60kg的该种水果,
可按5元/kg批发,
图②表示批发量高于60kg的该种水果,可按4元/kg批发;
(2)由题意得:![]() ,
,
函数图象如图所示.
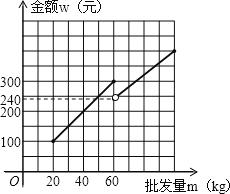
由图可知批发量超过60时,价格在4元中,
所以资金金额满足240<w≤300时,以同样的资金可批发到较多数量的该种水果;
(3)设日最高销售量为xkg(x>60),日零售价为p,
设x=pk+b,则由图②该函数过点(6,80),(7,40),
代入可得:x=320﹣40p,于是p=![]() ,
,
销售利润y=x(![]() ﹣4)=﹣
﹣4)=﹣![]() (x﹣80)2+160
(x﹣80)2+160
当x=80时,y最大值=160,
此时p=6,
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.

练习册系列答案
相关题目