题目内容
【题目】已知,在△ABC 中,∠A=90°,AB=AC,点 D 为 BC 的中点.
(1)点 E、F 分别为 AB、AC 上的中点,请按要求作出满足条件的△ABC 图形并证明:DE=DF;
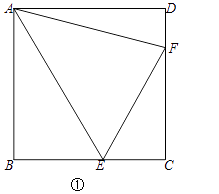
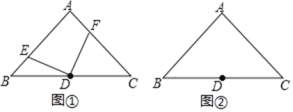
(2)如图①,若点 E、F 分别为 AB、AC 上的点,且 DE⊥DF,求证:BE=AF;
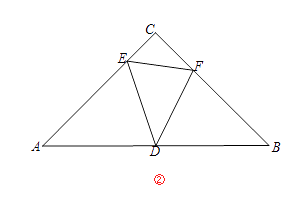
(3)若点 E、F 分别为 AB、CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图②说明理由.
【答案】(1)见解析;(2)见解析;(3) BE=AF,见解析.
【解析】
(1)画图并证明△AED≌△AFD,可得DE=DF;
(2)如图①,证明△BDE≌△ADF,可得BE=AF;
(3)如图②,证明△EDB≌△FDA,可得BE=AF.
(1)如图,连接AD.

∵∠A=90°,AB=AC,点D为BC的中点,∴∠EAD=∠FAD.
∵点E、F分别为AB、AC上的中点,∴AE![]() AB,AF
AB,AF![]() AC.
AC.
在△AED和△AFD中,∵ ,∴△AED≌△AFD(SAS),∴DE=DF;
,∴△AED≌△AFD(SAS),∴DE=DF;
(2)连接AD,如图①所示.
∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠B=45°.
∵点D为BC的中点,∴AD![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.
在△BDE和△ADF中,∵ ,∴△BDE≌△ADF(ASA),∴BE=AF;
,∴△BDE≌△ADF(ASA),∴BE=AF;
(3)BE=AF.证明如下:
连接AD,如图②所示.
∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.
∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,∴∠EDB=∠FDA.
在△EDB和△FDA中,∵ ,∴△EDB≌△FDA(ASA),∴BE=AF.
,∴△EDB≌△FDA(ASA),∴BE=AF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目