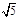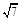题目内容
如图所示.P是⊙O外一点.PA是⊙O的切线.点A是切点.B是⊙O上一点.
且PA = PB,连接AO、BO、PO、AB,并延长BO与切线PA相交于点C.
(1)求证:PB是⊙O的切线 ;
(2)求证: AC ? PC=" OC" ? BC ;
(3)设∠AOC = ,若cos
,若cos =
=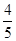 ,OC =" 15" ,求AB的长。
,OC =" 15" ,求AB的长。
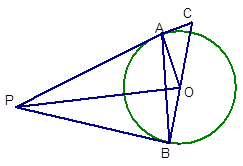
且PA = PB,连接AO、BO、PO、AB,并延长BO与切线PA相交于点C.
(1)求证:PB是⊙O的切线 ;
(2)求证: AC ? PC=" OC" ? BC ;
(3)设∠AOC =
 ,若cos
,若cos =
=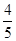 ,OC =" 15" ,求AB的长。
,OC =" 15" ,求AB的长。
(1)证明: ∵PA=PB,AO=BO,PO=PO
∴△APO≌△BPO ∴∠PBO=∠PAO=90°
∴PB是⊙O的切线
(2)证明:∵∠OAC=∠PBC=90°
∴△CPB∽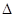 COA
COA
∴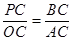 即AC?PC= OC?BC
即AC?PC= OC?BC
(3)解:cos =
=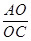 =
=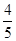 ∴AO=12
∴AO=12
∵△CPB∽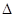 COA ∠BPC=∠AOC=
COA ∠BPC=∠AOC=
∴tan∠BPC=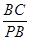 =
=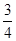 ∴PB=36 PO=12
∴PB=36 PO=12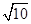
∵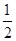 AB?PO= OB?BP ∴AB=
AB?PO= OB?BP ∴AB=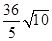
∴△APO≌△BPO ∴∠PBO=∠PAO=90°
∴PB是⊙O的切线
(2)证明:∵∠OAC=∠PBC=90°
∴△CPB∽
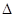 COA
COA∴
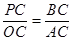 即AC?PC= OC?BC
即AC?PC= OC?BC(3)解:cos
 =
=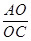 =
=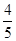 ∴AO=12
∴AO=12∵△CPB∽
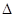 COA ∠BPC=∠AOC=
COA ∠BPC=∠AOC=
∴tan∠BPC=
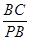 =
=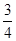 ∴PB=36 PO=12
∴PB=36 PO=12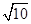
∵
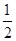 AB?PO= OB?BP ∴AB=
AB?PO= OB?BP ∴AB=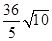
(1)连接OP,与AB交于点C.欲证明PB是⊙O的切线,只需证明∠OBP=90°即可;
(2)根据相似三角形的判定定理AA证明△CPB∽△COA,然后由相似三角形的对应边成比例求得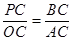 ,即AC?PC= OC?BC;
,即AC?PC= OC?BC;
(3)在Rt△OAQ中根据勾股定理和三角函数的余弦值的定义解得AO=12,利用△CPB∽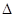 COA求出PB=36,OP=12
COA求出PB=36,OP=12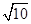 ;然后由切线的性质求AB的长.
;然后由切线的性质求AB的长.
(2)根据相似三角形的判定定理AA证明△CPB∽△COA,然后由相似三角形的对应边成比例求得
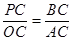 ,即AC?PC= OC?BC;
,即AC?PC= OC?BC;(3)在Rt△OAQ中根据勾股定理和三角函数的余弦值的定义解得AO=12,利用△CPB∽
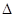 COA求出PB=36,OP=12
COA求出PB=36,OP=12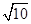 ;然后由切线的性质求AB的长.
;然后由切线的性质求AB的长.
练习册系列答案
相关题目
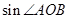 = .
= .
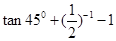 .
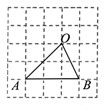
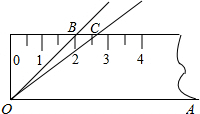
. 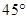 的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将
的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将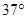 的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm
的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm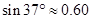 ,
,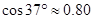 ,
,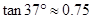 )
)
 。请计算停车位所占道路的宽度EF(结果精确到0.1米)。
。请计算停车位所占道路的宽度EF(结果精确到0.1米)。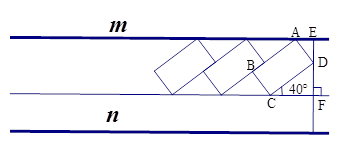
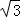 )、D(0,3
)、D(0,3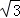 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.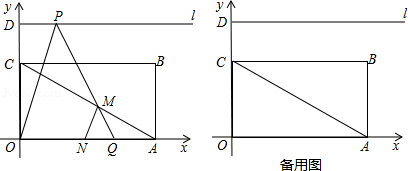
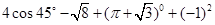
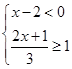
 中,
中,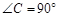 ,若
,若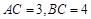 ,则
,则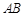 的值为( )
的值为( )