题目内容
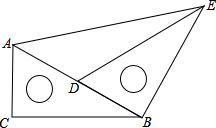 把两块含有30°的相同的直角尺按如图所示摆放,连接AE,若AC=6cm,则△ADE的面积是
把两块含有30°的相同的直角尺按如图所示摆放,连接AE,若AC=6cm,则△ADE的面积是分析:根据图可直接求出AB、BC的长度,从而求出AD的长,然后根据图找出△ADE的高,再求它的面积就容易了.
解答:解:∵AC=6cm,∠ABC=30°,
∴AB=12,
∴BC=
=6
,
在△ADE中,BE是△ADE的高,
∴S△ADE=
×AD×BE,
∵BD=6,AB=12,
∴AD=6,
∴S△ADE=
×AD×BE=
×6×6
=18
cm2,
故答案为18
cm2.
∴AB=12,
∴BC=
| 122-62 |
| 3 |
在△ADE中,BE是△ADE的高,
∴S△ADE=
| 1 |
| 2 |
∵BD=6,AB=12,
∴AD=6,
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为18
| 3 |
点评:本题考查了含30°角的直角三角形、勾股定理以及直角三角形的面积公式,解题时要结合图形会更容易.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
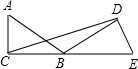 把两块含有30°角的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积等于( )
把两块含有30°角的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积等于( )A、9
| ||||
| B、18 | ||||
| C、27 | ||||
D、
|
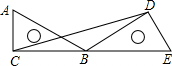 把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是
把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是 同一直线上,连接CD.
同一直线上,连接CD.

