题目内容
如图,把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在 同一直线上,连接CD.
同一直线上,连接CD.
(1)求∠DCB的度数;
(2)若AC=6cm,求△BCD的面积.
 同一直线上,连接CD.
同一直线上,连接CD.(1)求∠DCB的度数;
(2)若AC=6cm,求△BCD的面积.
分析:(1)意可知可以得到∠DBE=∠ABC=30°,然后利用等腰三角形的性质即可求出∠BCD的度数;
(2)利用直角三角形的性质和勾股定理解答即可.
(2)利用直角三角形的性质和勾股定理解答即可.
解答:解:(1)由题意可知△ACB≌△EDB,
∴CB=BD,
∵∠DBE=30°,
∴∠CBD=150°,
∴∠BCD=15°;
(2)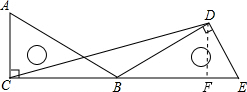 ∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°
∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°
∴
=
,cos∠ABC=cos30°=
=
∴AB=BE=2AC=2DE=2×6=12,BC=
×AB=
×12=6
∴BD=6
过D作DF⊥BE于点F,在Rt△BDF中,∠DBE=30°
∴
=
=
,DF=3
∴S△BCD=
BC•DF=
×6
×3
=27cm2.
∴CB=BD,
∵∠DBE=30°,
∴∠CBD=150°,
∴∠BCD=15°;
(2)
 ∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°
∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°∴
| AC |
| AB |
| 1 |
| 2 |
| BC |
| AB |
| ||
| 2 |
∴AB=BE=2AC=2DE=2×6=12,BC=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴BD=6
| 3 |
过D作DF⊥BE于点F,在Rt△BDF中,∠DBE=30°
∴
| DF |
| BD |
| DF | ||
6
|
| 1 |
| 2 |
| 3 |
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:(1)本题主要考查了三角形的外角度数以及等腰三角形的性质,难度适中;
(2)本题是一道根据直角三角形的性质结合勾股定理求解的综合题,求高DF除上述方法外,还可根据面积法列方程解答,同学们可以自己试一下.
(2)本题是一道根据直角三角形的性质结合勾股定理求解的综合题,求高DF除上述方法外,还可根据面积法列方程解答,同学们可以自己试一下.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
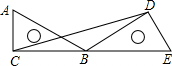 把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是
把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是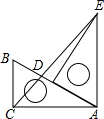 把两块含有30°的相同的直角尺按如图所示摆放,连接CE交AB于D.若BC=6cm,则①AB=
把两块含有30°的相同的直角尺按如图所示摆放,连接CE交AB于D.若BC=6cm,则①AB= 同一直线上,连接CD.
同一直线上,连接CD.