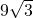Question

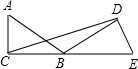把两块含有30°角的相同的直角三角尺按如图所示摆放，使点C、B、E在同一直线上，连接CD，若AC=6cm，则△BCD的面积等于（　　）

• A、9

  3

• B、18
• C、27
• D、

  9

  4

  3

Answer 1

分析：要求三角形的面积，首先找到三角形的高和底边，由题已知条件和根据几何图形证△ABC≌△EBD，从而求出三角形底边BC边上的高，从而求出面积．

解答：解：由已知得∠ABC=30°，AC=6cm，
∴BC=6

3

，AB=12，
因为两块含有30°角的相同的直角三角尺按如图所示摆放，
∴△ABC≌△EBD，BE=AB=12，S_△EBD=S_△ABC，
∵S_△ABC=

1

2

AC×BC=18

3

，
∴BC边上的高为3

3

，
此高即为△BCD的高，
∴S_△BCD=

1

2

×BC×3

3

=27．
故选C．

点评：此题考查应用解直角三角形求三角形的高及面积．