Question

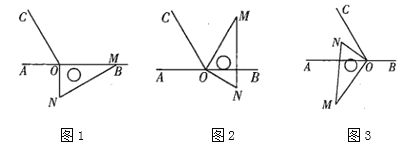
【题目】已知∠AOB＝100°，∠BOC＝60°，OM平分∠AOB，ON平分∠BOC，求∠MON的度数．

Answer 1

【答案】20°或80°

【解析】

注意此题要分两种情况：①当OC落在∠AOB的内部时，②当OC落在∠AOB的外部时；利用角的和差关系计算，

分两种情况计算：

①当OC落在∠AOB的内部时：

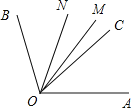
∵OM平分∠AOB，

∴∠AOM＝∠AOB＝×100°＝50°，

∵ON平分∠BOC，

∴∠BON＝∠BOC＝×60°＝30°，

∴∠MON＝∠AOB﹣∠AOM﹣∠BON＝100°﹣50°﹣30°＝20°，

②当OC落在∠AOB的外部时；

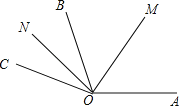
∵OM平分∠AOB，ON平分∠BOC，

∴∠BOM＝∠AOB＝×100°＝50°，

∠BON＝∠BOC＝×60°＝30°，

∴∠MON＝∠BOM+∠BON＝50°+30°＝80°

综上所述，∠MON的度数为20°或80°．