题目内容
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( ) 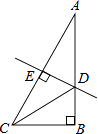
A.2 ![]()
B.2
C.4 ![]()
D.4
【答案】A
【解析】解:∵在Rt△ABC中,∠B=90°,∠A=30°,
∴∠ACB=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠DCB=60°﹣30°=30°,
在Rt△DBC中,∠B=90°,∠DCB=30°,BD=1,
∴CD=2BD=2,
由勾股定理得:BC= ![]() =
= ![]() ,
,
在Rt△ABC中,∠B=90°,∠A=30°,BC= ![]() ,
,
∴AC=2BC=2 ![]() ,
,
故选A.
求出∠ACB,根据线段垂直平分线的性质求出AD=CD,推出∠ACD=∠A=30°,求出∠DCB,即可求出BD、BC,根据含30°角的直角三角形性质求出AC即可.

练习册系列答案
相关题目