题目内容
【题目】端午节期间，某校“慈善小组”筹集到1240元善款，全部用于购买水果和粽子，然后到福利院送给老人，决定购买大枣粽子和普通粽子共20盒，剩下的钱用于购买水果，要求购买水果的钱数不少于180元但不超过240元．已知大枣粽子比普通粽子每盒贵15元，若用300元恰好可以买到2盒大枣粽子和4盒普通粽子．
（1）请求出两种口味的粽子每盒的价格；
（2）设买大枣粽子x盒，买水果共用了w元． ①请求出w关于x的函数关系式；
②求出购买两种粽子的可能方案，并说明哪一种方案使购买水果的钱数最多．
【答案】
（1）解：设买大枣粽子x元/盒，普通粽子y元/盒，
根据题意得， 
，
解得 
．
答：大枣粽子60元/盒，普通粽子45元/盒
（2）解：①设买大枣粽子x盒，则购买普通粽子（20﹣x）盒，买水果共用了w元，
根据题意得，w=1240﹣60x﹣45（20﹣x），
=1240﹣60x﹣900+45x，
=﹣15x+340，
故，w关于x的函数关系式为w=﹣15x+340；
②∵要求购买水果的钱数不少于180元但不超过240元，
∴ 
，
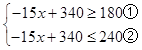解不等式①得，x≤10 
，
解不等式②得，x≥6 ，
所以，不等式组的解集是6 ≤x≤10 ，
∵x是正整数，
∴x=7、8、9、10，
可能方案有：
方案一：购买大枣粽子7盒，普通粽子13盒，
方案二：购买大枣粽子8盒，普通粽子12盒，
方案三：购买大枣粽子9盒，普通粽子11盒，
方案四：购买大枣粽子10盒，普通粽子10盒；
∵﹣15＜0，
∴w随x的增大而减小，
∴方案一可使购买水果的钱数最多，最多为﹣15×7+340=235元
【解析】（1）设买大枣粽子x元/盒，普通粽子y元/盒，根据两种粽子的单价和购买两种粽子用300元列出二元一次方程组，然后求解即可；（2）①表示出购买普通粽子的（20﹣x）盒，然后根据购买水果的钱数等于善款总数减去购买两种粽子的钱数，整理即可得解；②根据购买水果的钱数不少于180元但不超过240元列出不等式组，然后求解得到x的取值范围，再根据粽子的盒数是正整数从而写出所有的可能购买方案，再根据一次函数的增减性求出购买水果钱数最多的方案．
