题目内容
【题目】在直角坐标系中，点M，N在同一个正比例函数图象上的是（ ）
A.M（2，﹣3），N（﹣4，6）B.M（﹣2，3），N（4，6）
C.M（﹣2，﹣3），N（4，﹣6）D.M（2，3），N（﹣4，6）
【答案】A
【解析】
设正比例函数的解析式为y=kx，根据4个选项中得点M的坐标求出k的值，再代入N点的坐标去验证点N是否在正比例函数图象上，由此即可得出结论．
解：设正比例函数的解析式为y=kx，
A、﹣3=2k，解得：k=
，﹣4×（）=6，6=6，∴点N在正比例函数y=x的图象上；
B、3=﹣2k，解得：k=，4×（）=﹣6，﹣6≠6，∴点N不在正比例函数y=x的图象上；
C、﹣3=﹣2k，解得：k=
，4×=6，6≠﹣6，∴点N不在正比例函数y=x的图象上；
D、3=2k，解得：k=，﹣4×=﹣6，﹣6≠6，∴点N不在正比例函数y=x的图象上．
故选A．
“点睛”本题考查了一次函数图象上点的坐标以及待定系数法求函数解析式，解题的关键是
验证4个选项中点M、N是否在同一个正比例函数图象上. 本题属于基础题，难度不大，解决该题型题目时，根据给定的一点的坐标利用待定系数法求出正比例函数解析式，再代入另一点坐标去验证该点是否在该正比例函数图象上.
练习册系列答案
名校课堂系列答案
相关题目
【题目】问题：探究函数y＝x+
的图象和性质．
小华根据学习函数的方法和经验，进行了如下探究，下面是小华的探究过程，请补充完整：
（1）函数的自变量x的取值范围是：____；
（2）如表是y与x的几组对应值，请将表格补充完整：
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
（3）如图，在平面直角坐标系中描点并画出此函数的图象；
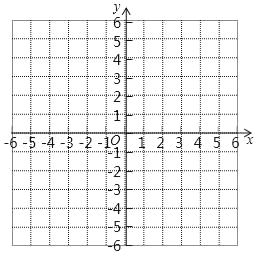
（4）进一步探究：结合函数的图象，写出此函数的性质（一条即可）．
