题目内容
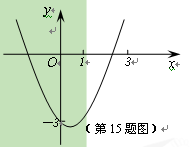
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)A点的坐标是 ;B点坐标是 ;
(2)直线BC的解析式是: ;
(3)点P是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积,若不存在,试说明理由;
(4)若点M在x轴上,点N在抛物线上,以A、C、M、N为顶点的四边形是平行四边形时,请直接写出点M点坐标.

【答案】(1)A(![]() ,0) B(8,0);(2)
,0) B(8,0);(2)![]() ; (3)存在点P,使△PBC的面积最大,最大面积是16 ;(4)(
; (3)存在点P,使△PBC的面积最大,最大面积是16 ;(4)(![]() ,0),(4, 0),(
,0),(4, 0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
![]() 可得a的值,求出解析式.由解析式可得出C和B的坐标,从而得出直线的解析式.运用假设法,连接辅助线可以设出P,D的坐标,表达出相应△PBC的面积解析式,分析可得出结果.由平行四边形的定义可求出答案.
可得a的值,求出解析式.由解析式可得出C和B的坐标,从而得出直线的解析式.运用假设法,连接辅助线可以设出P,D的坐标,表达出相应△PBC的面积解析式,分析可得出结果.由平行四边形的定义可求出答案.
(1)A(![]() ,0) B(8,0);
,0) B(8,0);
(2)![]() ;
;
(3)假设存在点P,连结PB、PC,过点P作PD∥y轴交直线BC于点D,
设点P(m,![]() )
)
则点D(m,![]() )
)
所以PD=![]()
![]()
=![]()
∴![]()
![]()
∵点P是直线BC上方的抛物线上的一动点(不与B、C重合)
∴![]()
∴当![]() 时,△PBC的面积最大,最大面积是16
时,△PBC的面积最大,最大面积是16
∴存在点P,使△PBC的面积最大,最大面积是16
(4)(![]() ,0),(4, 0),(
,0),(4, 0),(![]() ,0),(
,0),(![]() ,0) .
,0) .

练习册系列答案
相关题目