题目内容
如图①,直线AB的解析式为y=kx-2k(k<0)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.(1)求C点的坐标;
(2)如图②,过O1作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
(3)在(2)的条件下,连接OO1与⊙O1交于点G,点P为劣弧
 |
| GF |
 |
| GF |
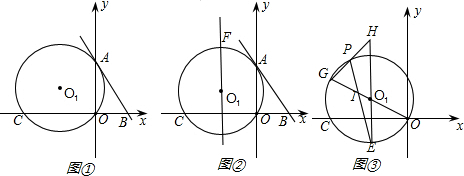
分析:(1)连接AC∵y=kx-2k∴B(2,0)∵∠ABO=60°∴∠OAB=30°∴AB=4,OA=2
,求出∠CAB=90°则可得出C点的坐标;
(2)取B点关于EF的对称点M,则M点的坐标为(-8,0),设直线AM的解析式为y=kx+b,求出解析式后再求直线AM与直线EF的交点即可;
(3)连接GF,证明△HGF≌△IEO1,即可得出O1H-O1I的值不发生变化.
| 3 |
(2)取B点关于EF的对称点M,则M点的坐标为(-8,0),设直线AM的解析式为y=kx+b,求出解析式后再求直线AM与直线EF的交点即可;
(3)连接GF,证明△HGF≌△IEO1,即可得出O1H-O1I的值不发生变化.
解答: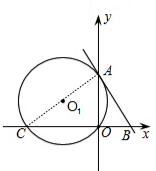 解:(1)连接AC
解:(1)连接AC
∵y=kx-2k∴B(2,0)
∵∠ABO=60°∴∠OAB=30°
∴AB=4,OA=2
∵AB是切线∴∠CAB=90°,∠ACB=30°
∴AC=4
,CO=6
∴C(-6,0).
(2)存在D点,坐标为D(-3,
)
∵EF过圆心且垂直x轴,
∴EF平分CO
取B点关于EF的对称点M,则M点的坐标为(-8,0)
设直线AM的解析式为y=kx+b
∵A(0,2
),M(-8,0)∴y=
x+2
直线AM与直线EF的交点即为D点,此时△DAB的周长最短
∴D(-3,
),
(3)O1H-O1I的值不发生变化,O1H-O1I=2
连接GF,
∵∠GOC=30°
∴∠OO1E=∠GO1F=60°
∴△GO1F为等边三角形
∴GF=O1E
∵∠HGF=∠HEP,∠HFG=∠EO1I=120°
∴△HGF≌△IEO1
∴HF=IO1
∴O1H-O1I=O1F=2
.
 解:(1)连接AC
解:(1)连接AC∵y=kx-2k∴B(2,0)
∵∠ABO=60°∴∠OAB=30°
∴AB=4,OA=2
| 3 |
∵AB是切线∴∠CAB=90°,∠ACB=30°
∴AC=4
| 3 |
∴C(-6,0).
(2)存在D点,坐标为D(-3,
| 5 |
| 4 |
| 3 |
∵EF过圆心且垂直x轴,
∴EF平分CO
取B点关于EF的对称点M,则M点的坐标为(-8,0)
设直线AM的解析式为y=kx+b
∵A(0,2
| 3 |
| ||
| 4 |
| 3 |
直线AM与直线EF的交点即为D点,此时△DAB的周长最短
∴D(-3,
| 5 |
| 4 |
| 3 |
(3)O1H-O1I的值不发生变化,O1H-O1I=2
| 3 |
连接GF,

∵∠GOC=30°
∴∠OO1E=∠GO1F=60°
∴△GO1F为等边三角形
∴GF=O1E
∵∠HGF=∠HEP,∠HFG=∠EO1I=120°
∴△HGF≌△IEO1
∴HF=IO1
∴O1H-O1I=O1F=2
| 3 |
点评:本题考查了一次函数的综合知识,难度较大,关键是巧妙作出辅助线进行解题.

练习册系列答案
相关题目
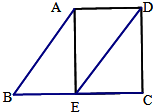
 22、完成下列证明:
22、完成下列证明:

 23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.
23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.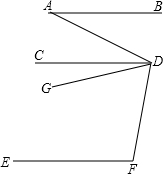
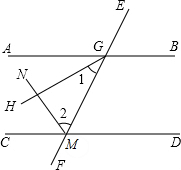 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.