题目内容
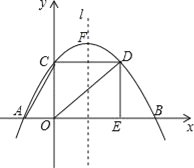
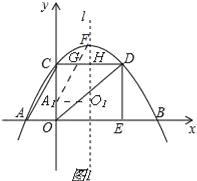
【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
【答案】(1)D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)
x+4;(2)![]() ;(3)当0<t≤3时,S=
;(3)当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】试题分析:(1)用待定系数法求抛物线解析式;(2)由GH∥A1O1,求出GH=1,再求出FH,S重叠部分=S△A1O1F﹣S△FGH计算即可;(3)分两种情况①直接用面积公式计算,②用面积差求出即可.
试题解析:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).
∴设抛物线的解析式为y=a(x+3)(x﹣9), ∵C(0,4)在抛物线上, ∴4=﹣27a,
∴a=﹣![]() , ∴设抛物线的解析式为y=﹣
, ∴设抛物线的解析式为y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y轴,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
(2)如图1, ∵点F是抛物线y=﹣![]() x2+
x2+![]() x+4的顶点,∴F(3,
x+4的顶点,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG,
∴S重叠部分=S△A1O1F﹣S△FGH=![]()
![]() A1O1×O1F﹣
A1O1×O1F﹣![]()
![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
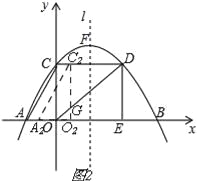
(3)①当0<t≤3时,如图2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
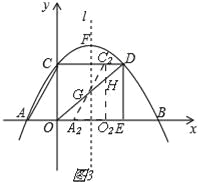
②当3<t≤6时,如图3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12.
t2﹣3t+12.

【题目】为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 | 分组 | 频数(人数) | 频率 |
1 | 10≤t<30 | 0.16 | |
2 | 30≤t<50 | 20 | |
3 | 50≤t<70 | 0.28 | |
4 | 70≤t<90 | 6 | |
5 | 90≤t<110 |
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?