题目内容
【题目】甲、乙两车同时从A地出发,匀速开往B地,甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动:当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h,设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.

(1)A、B两地的距离是 km,乙车的速度是 km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距50km时,直接写出x的值.
【答案】(1)600,75;(2)y=-225x+1200;(3)当两车相距50km时,x的值是![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据题意和函数图象中的数据,可知A、B两地的距离是150×4=600km,然后根据当甲车到达A地时,乙车恰好到达B地,可以得到乙车的速度;
(2)根据题意,可以求得点M的坐标,然后即可写出点M表示的实际意义,再根据函数图象中的数据,可以求得线段MN所表示的y与x之间的函数表达式;
(3)根据题意和函数图象中的数据,可以求得当两车相距50km时,对应的x的值.
(1)由图象可得,
A、B两地的距离是150×4=600(km),
乙车的速度为:150÷2=75(km/h),
故答案为:600,75;
(2)600÷150=4小时
(150-75)×4=75×4=300(km),
点M的实际意义是,在两车行驶4小时时,甲车到达B地,此时甲乙两车的距离是300km,
即点M的坐标为(4,300),
点N的横坐标为:600×2÷(150+75)=![]() ,
,
即点N的坐标为(![]() ,0),
,0),
设线段MN所表示的y与x之间的函数表达式为y=kx+b,
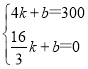 ,得
,得![]() ,
,
即线段MN所表示的y与x之间的函数表达式为y=-225x+1200;
(3)当0≤x≤4时,
(150-75)x=50,
解得x=![]() ;
;
当4<x≤![]() 时,
时,
(150+75)x+50=600×2,
解得,x=![]() ;
;
当x>![]() 时,
时,
(150+75)x-50=600×2,
解得,x=![]() ;
;
由上可得,当两车相距50km时,x的值是![]() 或
或![]() 或
或![]() .
.

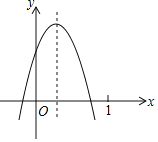
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5