题目内容
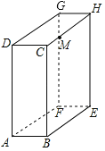
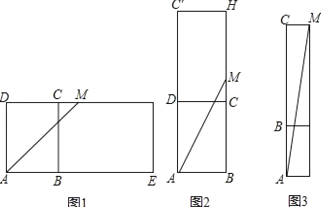
【题目】如图,长方体的长BE=20cm,宽AB=10cm,高AD=15cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
首先将长方体沿CH、HE、BE剪开,向右翻折,使面ABCD和面BEHC在同一个平面内,连接AM;或将长方体沿CH、C′D、C′H剪开,向上翻折,使面ABCD和面DCHC′在同一个平面内,连接AM,或将长方体沿AB、AF、EF剪开,向下翻折,使面CBEH和下面在同一个平面内,连接AM,然后分别在Rt△ADM与Rt△ABM与Rt△ACM,利用勾股定理求得AM的长,比较大小即可求得需要爬行的最短路程.
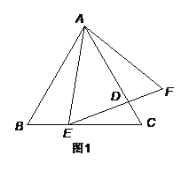
解:将长方体沿CH、HE、BE剪开,向右翻折,使面ABCD和面BEHC在同一个平面内,连接AM,如图1,
由题意可得:MD=MC+CD=5+10=15cm,AD=15cm,
在Rt△ADM中,根据勾股定理得:AM=15![]() cm;
cm;
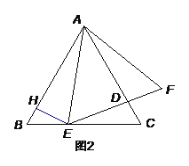
将长方体沿CH、C′D、C′H剪开,向上翻折,使面ABCD和面DCHC′在同一个平面内,连接AM,
如图2,
由题意得:BM=BC+MC=5+15=20(cm),AB=10cm,
在Rt△ABM中,根据勾股定理得:AM=10![]() cm,
cm,
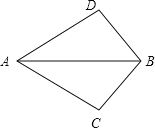
连接AM,如图3,
由题意得:AC=AB+CB=10+15=25(cm),MC=5cm,
在Rt△ACM中,根据勾股定理得:AM=5![]() cm,
cm,
∵15![]() <10
<10![]() <5
<5![]() ,
,
则需要爬行的最短距离是15![]() cm.
cm.
故选A.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】某市居民使用自来水按如下标准收费(水费按月缴纳)
月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户用了
时,某用户用了![]() 水,求该用户这个月应该缴纳的水费;
水,求该用户这个月应该缴纳的水费;
(2)设某用户用水量为![]() 立方米,求该用户应缴纳的水费(用含
立方米,求该用户应缴纳的水费(用含![]() 的式子表达)
的式子表达)