Question

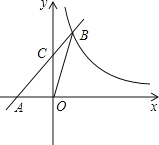
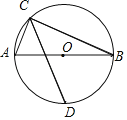
【题目】如图，AB是⊙O的直径，点C是⊙O上一点（点C不与A，B重合），连接CA，CB．∠ACB的平分线CD与⊙O交于点D．

（1）求∠ACD的度数；

（2）探究CA，CB，CD三者之间的等量关系，并证明；

（3）E为⊙O外一点，满足ED＝BD，AB＝5，AE＝3，若点P为AE中点，求PO的长．

Answer 1

【答案】（1）∠ACD＝45°；（2）BC+AC＝CD，见解析；（3）OP＝．

【解析】

（1）由圆周角的定义可求∠ACB＝90°，再由角平分线的定义得到∠ACD＝45°；

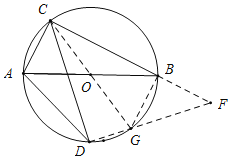
（2）连接CO延长与圆O交于点G，连接DG、BG，延长DG、CB交于点F；先证明△BGF是等腰直角三角形，得到BG＝BF，AG＝BF，再证明△CDF是等腰三角三角形，得到CF＝CD，即可求得BC+AC＝CD；

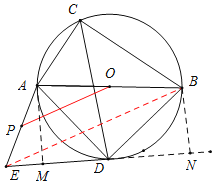
（3）过点A作AM⊥ED，过点B作BN⊥ED交ED延长线与点N，连接BE；先证明Rt△AMD≌Rt△DNB（AAS），再证明△AED是等腰三角形，分别求得EN＝，BN＝，在Rt△EBN中，BE＝，OP＝BN＝．

解：（1）∵AB是直径，点C在圆上，

∴∠ACB＝90°，

∵∠ACB的平分线CD与⊙O交于点D，

∴∠ACD＝45°；

（2）BC+AC＝CD，

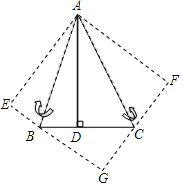
连接CO延长与圆O交于点G，连接DG、BG，延长DG、CB交于点F；

∴∠CDG＝∠CBG＝90°，

∵∠ACB＝90°，

∴AC∥BG，

∴∠CGB＝∠ACG，

∴∠CGB＝45°+∠DCG，

∵∠CBF＝90°+∠DCG，

∴∠BGF＝45°，

∴△BGF是等腰直角三角形，

∴BG＝BF，

∵△ACO≌△BGO（SAS），

∴AG＝BF，

∵△CDF是等腰三角三角形，

∴CF＝CD，

∴BC+AC＝CD；

（3）过点A作AM⊥ED，过点B作BN⊥ED交ED延长线与点N，连接BE；

∵∠ACD＝∠ABD＝45°，∠ADB＝90°，

∴AD＝BD，

∵AB＝5，

∴BD＝AD＝，

∵∠MAD＝∠BDN，

∴Rt△AMD≌Rt△DNB（AAS），

∴AM＝DN，MD＝BN，

∵ED＝BD，

∴△AED是等腰三角形，

∵AE＝3，

∴AM＝，DM＝，

∴EN＝，BN＝，

在Rt△EBN中，BE＝，

∵P是AE的中点，O是AB的中点，

∴OP＝BN，

∴OP＝．