题目内容
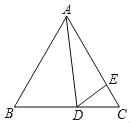
【题目】如图,已知抛物线![]() 过点
过点![]() ,
,![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段![]() 与
与![]() 的数量关系(
的数量关系(![]() 、
、![]() 、
、![]() ),并证明你的判断;
),并证明你的判断;
(3)![]() 为
为![]() 轴上一点,以
轴上一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点![]() ,求自然数
,求自然数![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]() ;(3)6
;(3)6
【解析】
(1)利用待定系数法求抛物线解析式;
(2)设B(![]() ,
,![]() ),而F(0,2),利用两点间的距离公式得到
),而F(0,2),利用两点间的距离公式得到![]() ,再利用配方法可得到
,再利用配方法可得到![]() ,由于BC=
,由于BC=![]() ,所以BF=BC;
,所以BF=BC;
(3)利用菱形的性质得到CB=CF=PF,加上CB=FB,则可判断△BCF为等边三角形,所以∠BCF=60°,则∠OCF=30°,于是可计算出CF=4,所以PF=CF=4,从而得到自然数m的值为6;
解:(1)把点(2,2),(4,5)代入![]() 得
得![]() ,
,
解得:![]()
所以抛物线解析式为![]() ;
;
(2)BF=BC.
理由如下:
设B(![]() ,
,![]() ),而F(0,2),
),而F(0,2),
∴![]() ,
,
∴![]() ,
,
∵BC⊥x轴,
∴BC=![]() ,
,
∴BF=BC;
(3)如图,
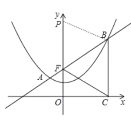
m为自然数,
则点P在F点上方,
∵以B、C、F、P为顶点的四边形是菱形,
∴CB=CF=PF,
而CB=FB,
∴BC=CF=BF,
∴△BCF为等边三角形,
∴∠BCF=60°,
∴∠OCF=30°,
在![]() 中,CF=2OF=4,
中,CF=2OF=4,
∴PF=CF=4,
span>∴P(0,6),
即自然数m的值为6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目