题目内容
【题目】在平面直角坐标系中,点![]() ,点
,点![]() 在
在![]() 轴上,以点
轴上,以点![]() 为直角顶点作等腰直角
为直角顶点作等腰直角![]() ..当点
..当点![]() 落在某函数的图象上时,称点
落在某函数的图象上时,称点![]() 为该函数的“悬垂点”,
为该函数的“悬垂点”,![]() 为该函数的“悬垂等腰直角三角形”.
为该函数的“悬垂等腰直角三角形”.
(1)若点![]() 是函数
是函数![]() 的悬垂点,直接写出点
的悬垂点,直接写出点![]() 的横坐标为________.
的横坐标为________.
(2)若反比例函数![]()
![]() 的悬垂等腰直角三角形面积是
的悬垂等腰直角三角形面积是![]() ,求
,求![]() 的值.
的值.
(3)对于函数![]() ,当
,当![]()
![]() 时,该函数的悬垂点只有一个,求
时,该函数的悬垂点只有一个,求![]() 的取值范围.
的取值范围.
(4)若函数![]() 的悬垂等腰直角
的悬垂等腰直角![]() 的面积范围为
的面积范围为![]() ,且点
,且点![]() 在第一象限,直接写出
在第一象限,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)6或2;(3)
;(2)6或2;(3)![]() ;(4)1≤a≤2或4≤a≤5.
;(4)1≤a≤2或4≤a≤5.
【解析】
(1)设C(m,![]() m+3),根据“悬垂等腰直角三角形”的定义可知∠CAB=45°,求出直线CA的解析式,C点即函数的图象与直线CA的交点,列方程求解即可;
m+3),根据“悬垂等腰直角三角形”的定义可知∠CAB=45°,求出直线CA的解析式,C点即函数的图象与直线CA的交点,列方程求解即可;
(2)先根据“悬垂等腰直角三角形”定义及悬垂等腰直角三角形面积是2,求得点C的坐标,再根据反比例函数概念求k的值;
(3)设点C(m,m﹣1),根据“悬垂等腰直角三角形”定义可列方程m2﹣5m+7=m﹣1,求解后再根据“该函数的悬垂点只有一个”即可求得结论;
(4)根据“点C在第一象限,2≤S△ABC≤![]() ”,可得2≤AB≤3,进而得到,3≤m≤4,再由“悬垂等腰直角三角形”定义可得,m2﹣2am+a2+a﹣3=m﹣1,解得:a1=m﹣2或a2=m+1,即可得到结论.
”,可得2≤AB≤3,进而得到,3≤m≤4,再由“悬垂等腰直角三角形”定义可得,m2﹣2am+a2+a﹣3=m﹣1,解得:a1=m﹣2或a2=m+1,即可得到结论.
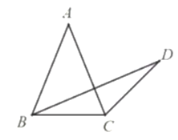
解:以点B为直角顶点作等腰直角△ABC,点A(1,0),即直线AC与x轴成45°角,与y=x或y=﹣x平行,
∴直线CA的解析式为:y=x﹣1或y=﹣x+1,
(1)当直线CA的解析式为y=x﹣1时,
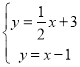 ,
,
解得:![]() ;
;
即C点为(8,7),
当直线CA的解析式为y=﹣x+1时,
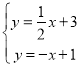 ,
,
解得: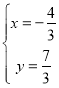 ;
;
即C点为(![]() ,
,![]() ),
),
故答案为:8或![]() ;
;
(2)设点C的横坐标为m,则点C的纵坐标为m﹣1,
∵S△ABC=![]() (m﹣1)2=2,
(m﹣1)2=2,
∴m1=﹣1,m2=3,
∴点C的坐标为(﹣1,﹣2)或(3,2),
∵点C在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=2或k=6;
(3)设点C(m,m﹣1),
∵点C在函数y=x2﹣5x+7的图象上,
∴m2﹣5m+7=m﹣1,
解得:m1=2,m2=4,
∵当1≤x≤n(n>1)时,该函数的悬垂点只有一个,
∴2≤n<4.
(4)∵点C在第一象限,2≤S△ABC≤![]() ,
,
∴2≤AB≤3,
∵点A(1,0),
∴3≤m≤4,
∵m2﹣2am+a2+a﹣3=m﹣1,
∴a1=m﹣2或a2=m+1,
当a=m﹣2时,可得1≤a≤2,
当a=m+1时,可得4≤a≤5,
综上所述,a的取值范围为:1≤a≤2或4≤a≤5.