题目内容
【题目】定义:三角形三条内角平分线的交点叫做三角形的内心;
性质:内心到三角形三边的距离相等.
如图1,点 ![]() 为
为 ![]() 的内心,
的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() ,则有
,则有 ![]() .
.
问题:如何求 ![]() 的值呢?
的值呢?
探究:
(1)小明思路:设△ABC的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,利用
,利用 ![]() 可求
可求 ![]() .
.
①图1中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,请你根据小明的思路求出
,请你根据小明的思路求出 ![]() 的值;
的值;
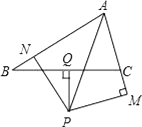
②如图2,△ABC中, ![]() ,设
,设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为 △ABC的内心,
为 △ABC的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() .若设
.若设 ![]() ,请用含
,请用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(2)小亮思路:“凡角平分处,必有轴对称”. 如图2,易得: ![]() ,
, ![]() ,
, ![]() . 请你根据小亮的思路,用含
. 请你根据小亮的思路,用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(3)①根据上述所列两式,求证: ![]() ;
;
②应用:已知一个直角三角形的两直角边长分别为 ![]() 和
和 ![]() ,求该三角形的内心到任意一边的距离
,求该三角形的内心到任意一边的距离 ![]() .
.
【答案】
(1)解:①由 ![]() 得,
得, ![]()
即 ![]() ,
,![]() ,
, ![]()
② ![]()
(2)![]()
(3)
①证明:由 ![]() 得,
得,
![]() ,
,
![]() ,
,
![]() ,则
,则 ![]()
②解:由 ![]() ,
, ![]() 得,
得, ![]() ,
,
则 ![]() ,或
,或 ![]()
【解析】此题考查三角形的内切圆与内心,利用内角平分线的性质,结合三角形的面积和差,推导出d的表达式.
【考点精析】关于本题考查的三角形的内切圆与内心,需要了解三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能得出正确答案.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案【题目】如图,某电视台的娱乐节目《周末打放送》有这样的翻奖牌游戏,数字的背面写有祝福语或奖金数,游戏规则是:每翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福.
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
正面
祝你开心 | 万事如意 | 奖金800元 |
身体健康 | 心想事成 | 奖金500元 |
奖金200元 | 生活愉快 | 谢谢参与 |
反面
计算:
(1)“翻到奖金800元”的概率;
(2)“翻到奖金”的概率;
(3)“翻不到奖金”的概率.