Question

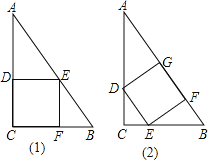
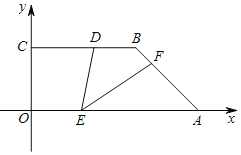
【题目】如图，BC⊥y轴，BC＜OA，点A，点C分别在x轴、y轴的正半轴上，D是线段BC上一点，BD=OA=，AB=3，∠OAB=45°，E，F分别是线段OA，AB上的两动点，且始终保持∠DEF=45°．将△AEF沿一条边翻折，翻折前后两个三角形组成的四边形为菱形，则线段OE的值为______．

Answer 1

【答案】或3或3．

【解析】

分类讨论,根据AE、AF、EF为对称轴进行翻折,展开讨论,见详解.

解：如上图连接OD,过点B作BH⊥OA于H,

由题可知,BD=,OA=4,

∵∠DEF=45°．

∴BH=OC=,CD=,OD=3,

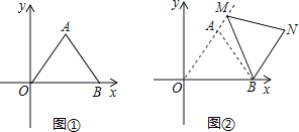
①如下图

若沿着AE进行翻折,即EF=AF, 此时F落在x轴下方点N处,四边形ANEF为正方形

∴∠A=∠AEF=45°,△AEF为等腰直角三角形,

∵∠DEF=45°,

∴DE⊥OA,

∴△OED是等腰直角三角形,OD=AB=3,

∴OE=,

②若沿着AF进行翻折,即AE=EF,此时点F与B重合,E点落在N点处,如下图

此时∠BDE=45°,四边形ABDE是平行四边形,

∴AE=BD=,

∴OE=OA-AE=4=3,

③若沿着EF进行翻折,即AE=AF,如下图

∵∠A=45°,

∴此时△EAF为等腰直角三角形,

∵易证△DOE∽△AEF

∴OE=OD=3

综上,OE=或3或3．