题目内容
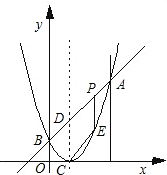 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.(1)求b的值及这个二次函数的关系式;
(2)设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)若点D为直线AB与该二次函数的图象对称轴的交点,则四边形DCEP能否构成平行四边形?如果能,请求出此时P点的坐标;如果不能,请说明理由.
(4)以PE为直径的圆能否与y轴相切?如果能,请求出点P的坐标;如果不能,请说明理由.
分析:(1)可用顶点式二次函数通式设出二次函数的解析式,然后将A点的坐标代入其中,即可求出抛物线的解析式和b的值.
(2)PE的长实际是直线AB的解析式与抛物线的差.由此可得出h,x的函数关系式.
(3)先求出D点的坐标和CD的长,由于四边形PDCE是平行四边形,因此CD=PE,将CD的长代入(2)的函数关系式中,可得出一个关于x的方程,如果方程无解,则说明不存在这样的P点,如果有解,那么求出的x就是P的横坐标,进而可根据直线AB的解析式求出P点的坐标.
(4)假设存在这样的P点,那么此时圆心到y轴的距离为
PE,即圆心的横坐标(即P的横坐标)为
h,然后代入(2)的函数式中即可求出P点的横坐标,进而可求出符合条件的P点的坐标.
(2)PE的长实际是直线AB的解析式与抛物线的差.由此可得出h,x的函数关系式.
(3)先求出D点的坐标和CD的长,由于四边形PDCE是平行四边形,因此CD=PE,将CD的长代入(2)的函数关系式中,可得出一个关于x的方程,如果方程无解,则说明不存在这样的P点,如果有解,那么求出的x就是P的横坐标,进而可根据直线AB的解析式求出P点的坐标.
(4)假设存在这样的P点,那么此时圆心到y轴的距离为
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)b=1
设抛物线的解析式为y=a(x-1)2把A(3,4)代入,
得a=1;
∴抛物线的解析式为y=(x-1)2
即y=x2-2x+1;
(2)h=(x+1)-(x2-2x+1)=-x2+3x(0<x<3);
(3)要使四边形DCEP是平行四边形,必须有PE=DC,
∵y=x+1经过点D,
∴D(1,2),
∴-x2+3x=2,
解得x=2或x=1,
∵当x=1时,y=2,
∴P(1,2)与D点重合,故舍去,
∴当点P的坐标为(2,3)时,四边形DCEP是平行四边形;
(4)设圆心坐标为(m,n),则m=
h时,该圆与y轴相切,
∵m=x,
∴得x=
,
解得x=1,x=0(舍去),
∴点P的坐标为(1,2)时,以PE为直径的圆能与y轴相切.
设抛物线的解析式为y=a(x-1)2把A(3,4)代入,
得a=1;
∴抛物线的解析式为y=(x-1)2
即y=x2-2x+1;
(2)h=(x+1)-(x2-2x+1)=-x2+3x(0<x<3);
(3)要使四边形DCEP是平行四边形,必须有PE=DC,
∵y=x+1经过点D,
∴D(1,2),
∴-x2+3x=2,
解得x=2或x=1,
∵当x=1时,y=2,
∴P(1,2)与D点重合,故舍去,
∴当点P的坐标为(2,3)时,四边形DCEP是平行四边形;
(4)设圆心坐标为(m,n),则m=
| 1 |
| 2 |
∵m=x,
∴得x=
| -x2+3x |
| 2 |
解得x=1,x=0(舍去),
∴点P的坐标为(1,2)时,以PE为直径的圆能与y轴相切.
点评:本题主要考查了一次函数与二次函数解析式的确定,平行四边形的判定和性质,切线的判定等知识点.
考查学生数形结合的数学思想方法.
考查学生数形结合的数学思想方法.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
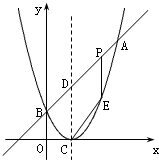 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.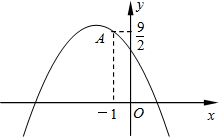 (2012•高淳县一模)如图,已知二次函数y=-
(2012•高淳县一模)如图,已知二次函数y=-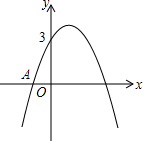 (2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
(2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
 如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.