题目内容
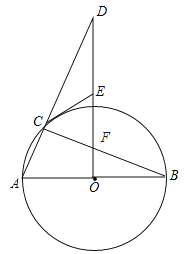
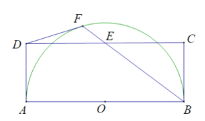
【题目】如图,在矩形ABCD中,边AB是半圆O的直径,点E是CD的中点,BE交半圆O于点F,连接DF.
(1)求证:DF是半圆O的切线;
(2)若AB =8,AD =3,求BF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OF、OD、AF,根据矩形的性质和已知条件可得DE=![]() CD,OB=
CD,OB=![]() AB,DC∥AB,∠OAD=90°,然后利用SAS证出△AOD≌△FOD,即可证出∠OAD=∠OFD=90°,然后根据切线的判定定理即可证出结论;
AB,DC∥AB,∠OAD=90°,然后利用SAS证出△AOD≌△FOD,即可证出∠OAD=∠OFD=90°,然后根据切线的判定定理即可证出结论;
(2)根据相似三角形的判定证出Rt△AOD∽Rt△FBA,然后列出比例式,根据比例式设AF=3x,BF=4x,然后根据勾股定理列出方程即可求出结论.
(1)证明:连接OF、OD、AF,

在矩形ABCD中,
∵点E是CD的中点,点O是AB的中点,
∴DE=![]() CD,OB=
CD,OB=![]() AB,DC∥AB,∠OAD=90°
AB,DC∥AB,∠OAD=90°
∴四边形OBED为平行四边形
∴OD∥BF
∴∠AOD=∠OBF,∠OFB=∠FOD
∵OB=OF
∴∠OBF=∠OFB
∴∠AOD=∠FOD,
∵OA=OF,OD=OD
∴△AOD≌△FOD(SAS)
∴∠OAD=∠OFD=90°,
∴OF⊥DF,即DF为半圆O的切线
(2)由(1)知:在Rt△AOD和Rt△FBA中,
∠AOD=∠OBF,∠DAO=∠BFA=90°
∴Rt△AOD∽Rt△FBA
∴![]()
又在矩形ABCD中,AB=8,AD=3,则OA=4,
∴![]()
∴可设AF=3x,BF=4x
在Rt△ABF中,AB2=AF2+BF2
82=(3x)2+(4x)2
解得,x1=![]() ,x2=-
,x2=-![]() (舍)
(舍)
即BF=![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于