题目内容
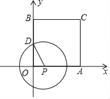
【题目】如图,正方形AOBC的顶点O在原点,边AO,BO分别在x轴和y轴上,点C坐标为(4,4),点D是BO的中点,点P是边OA上的一个动点,连接PD,以P为圆心,PD为半径作圆,设点P横坐标为t,当⊙P与正方形AOBC的边相切时,t的值为_____.
【答案】![]() 或2
或2![]()
【解析】
由点C的坐标可得OA、OB的长,根据点D是OB的中点可得OD的长,分⊙P与AC相切和⊙P与BC相切两种情况分别进行讨论即可求得答案.
∵点C坐标为(4,4),点D是BO的中点,
∴OA=OB=4,OD=![]() OB=2,
OB=2,
分⊙P与AC相切和⊙P与BC相切两种情况考虑:
①当⊙P与AC相切时,如图1所示.
∵点P横坐标为t,
∴PA=4﹣t.
在Rt△DOP中,OD=2,OP=t,PD=PA=4﹣t,
∴PD2=OD2+OP2,即(4﹣t)2=22+t2,
解得:t=![]() ;
;
②当⊙P与BC相切时,设切点为E,连接PE,如图2所示.
∵PE⊥BC,AC⊥BC,
∴PE∥AC.
∵PA∥EC,
∴四边形ACEP为矩形,
∴PE=AC=4,
∴PD=PE=4.
在Rt△POD中,OP=t,OD=2,PD=4,
∴PD2=OD2+OP2,即42=22+t2,
解得:t1=2![]() ,t2=﹣2
,t2=﹣2![]() (不合题意,舍去),
(不合题意,舍去),
综上所述:t的值为![]() 或2
或2![]() ,
,
故答案为:![]() 或2
或2![]() .
.

练习册系列答案
相关题目