题目内容
【题目】探究;
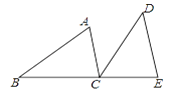
(![]() )如图,
)如图, ![]() 、
、![]() 为
为![]() 的边
的边![]() 、
、![]() 上的两定点,在
上的两定点,在![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最短.(不写作法)
的周长最短.(不写作法)

(![]() )如图,矩形
)如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,求四边形
上的动点,求四边形![]() 周长的最小值.
周长的最小值.

(![]() )如图,正方形
)如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边中点,在边
边中点,在边![]() 、
、![]() 、
、![]() 上分别确定点
上分别确定点![]() 、
、![]() 、
、![]() .使得四边形
.使得四边形![]() 周长最小,并求出最小值.
周长最小,并求出最小值.

【答案】(1)作图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)
试题分析:(1)利用轴对称图形的性质,作点P关于BC的对称点P′,连接P′Q,交BC于点M,则M是所求的点;(2)如图,延长EB至E'使E' B=EB,延长FD至F'使F' D=FD,连接E' F'交BC、CD于M、N.此时四边形EFNM周长最小.根据勾股定理求得EF、E' F'的长,即可得四边形OMNP周长的最小值;(3)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .作
.作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .连
.连![]() 交
交![]() 于
于![]() ,即为周长最小.根据正方形的性质和轴对称的性质易得
,即为周长最小.根据正方形的性质和轴对称的性质易得![]() 、
、![]() 、
、![]() 为各边中点,所以四边形
为各边中点,所以四边形![]() 周长的最小值为
周长的最小值为![]() .
.
试题解析:
(![]() )如图,作点
)如图,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是所求的点.
是所求的点.
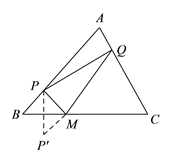
(![]() )如图,延长
)如图,延长![]() 至
至![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .此时四边形
.此时四边形![]() 周长最小.
周长最小.
周长![]()
![]()
![]() .
.
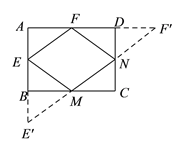
(![]() )如图,延长
)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .
.
作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .
.
连![]() 交
交![]() 于
于![]() ,即为周长最小.
,即为周长最小.
易得![]() 、
、![]() 、
、![]() 为各边中点,周长为
为各边中点,周长为![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(1)该商场购进A、B两种商品各多少件;
(2)商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原售价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?