题目内容
 如图,AB、CD相交于点O,∠A=∠C,EO=FO,∠1=∠2,试说明:DO=BO.
如图,AB、CD相交于点O,∠A=∠C,EO=FO,∠1=∠2,试说明:DO=BO.
证明:∵∠A=∠C,EO=FO,∠1=∠2;
∴△AEO≌△CFO,
∴∠AOE=∠COF,
又∠AOD=∠BOC,
∴∠EOD=∠FOB,
∵∠1=∠2,
∴∠DEO=∠OFB,
又EO=FO,
∴△EOD≌△FOB.
∴DO=BO.
分析:根据已知可知,∠A=∠C,EO=FO,∠1=∠2,可证△AEO≌△CFO,所以EO=OF,又可证∠EOD=∠FOB,得证△EOD≌△FOB,可证DO=BO.
点评:本题主要考查了全等三角形的判定及其结论的应用,得到∠EOD=∠FOB是正确解决本题的关键.
∴△AEO≌△CFO,
∴∠AOE=∠COF,
又∠AOD=∠BOC,
∴∠EOD=∠FOB,
∵∠1=∠2,
∴∠DEO=∠OFB,
又EO=FO,
∴△EOD≌△FOB.
∴DO=BO.
分析:根据已知可知,∠A=∠C,EO=FO,∠1=∠2,可证△AEO≌△CFO,所以EO=OF,又可证∠EOD=∠FOB,得证△EOD≌△FOB,可证DO=BO.
点评:本题主要考查了全等三角形的判定及其结论的应用,得到∠EOD=∠FOB是正确解决本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
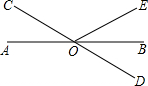 如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是
如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是 如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是
如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.
已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.