题目内容
 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.(1)求△ABC中BC上的高AH;
(2)求y与x之间的函数关系;
(3)当矩形的长x取何值时,这个矩形的面积最大?
分析:(1)利用勾股定理列式求出斜边BC的长,再根据三角形的面积列式进行计算即可得解;
(2)设DE为a,根据相似三角形对应高的比等于相似比列式用x表示出a,再根据矩形的面积列式整理即可;
(3)把y、x的函数关系式整理成顶点式解析式,再根据二次函数的最值问题解答即可.
(2)设DE为a,根据相似三角形对应高的比等于相似比列式用x表示出a,再根据矩形的面积列式整理即可;
(3)把y、x的函数关系式整理成顶点式解析式,再根据二次函数的最值问题解答即可.
解答:解:(1)∵AB=300米,AC=400米,
∴BC=
=500米,
∵AH是直角三角形的斜边上的高,
∴AH=
=240米;
(2)设DE=a,∵△ADG∽△ABC,
∴
=
,
即
=
,
∴a=-
x+240,
∴y=x(-
x+240)=-
x2+240x;
(3)y=-
x2+240x=-
(x-250)2+3000,
∴当x=250时,y取得最大值为3000.
∴BC=
| 3002-4002 |
∵AH是直角三角形的斜边上的高,
∴AH=
| 300×400 |
| 500 |
(2)设DE=a,∵△ADG∽△ABC,
∴
| AH-a |
| AH |
| DG |
| BC |
即
| 240-a |
| 240 |
| x |
| 500 |
∴a=-
| 12 |
| 25 |
∴y=x(-
| 12 |
| 25 |
| 12 |
| 25 |
(3)y=-
| 12 |
| 25 |
| 12 |
| 25 |
∴当x=250时,y取得最大值为3000.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应高的比等于相似比,勾股定理的应用,二次函数的最值问题,(2)求出矩形的宽DE是解题的关键.

练习册系列答案
相关题目
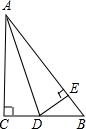 如图,有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则△DEB的面积为( )
如图,有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则△DEB的面积为( )| A、250cm2 | B、150cm2 | C、200cm2 | D、100cm2 |
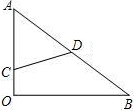 如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是
如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是 如图,有一块直角三角形纸片,其中∠C=90°,AC=6cm,BC=8,D为BC上一点,现将其沿AD折叠,使点C落在斜边AB的E处,则CD=
如图,有一块直角三角形纸片,其中∠C=90°,AC=6cm,BC=8,D为BC上一点,现将其沿AD折叠,使点C落在斜边AB的E处,则CD= 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角三角形纸片沿直线AD折叠,使点C恰好落在斜边AB上点E处.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角三角形纸片沿直线AD折叠,使点C恰好落在斜边AB上点E处.