题目内容
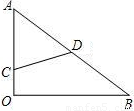
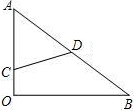 如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是
如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是分析:由勾股定理知,AB=
=5,当C点与点O或点A重合时,到点D的距离最大,根据直角三角形中斜边上的中线等于斜边的一半知,OD=AD=
AB=2.5,当DC⊥AO时,线段CD是从点D到AO的垂线段,长最小,此时CD是中位线,CD=
OB=2,所以2≤x≤2.5.
| a2+b2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:在Rt△OAB中,AB=
=5
当C点与点或点A重合时,CD的长最大
∴OD=AD=
AB=2.5
当DC⊥AO时,线段CD长最小,此时CD是中位线
∴CD=
OB=2
∴2≤x≤2.5.
| 32+42 |
当C点与点或点A重合时,CD的长最大
∴OD=AD=
| 1 |
| 2 |
当DC⊥AO时,线段CD长最小,此时CD是中位线
∴CD=
| 1 |
| 2 |
∴2≤x≤2.5.
点评:本题利用了勾股定理和三角形的中位线求解.注意点C在点A或点O是x是最大的,CD是从点D到AO的垂线段时,x是最小的.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.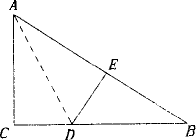
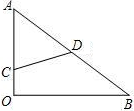 如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是________.
如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是________.