题目内容
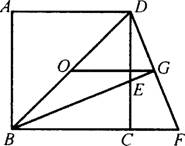
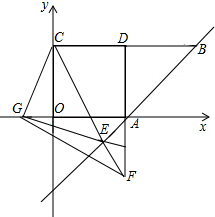
已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
(1)说明:△BCE≌△DCF;
(2)OG与BF有什么数量关系?说明你的结论;
 (3)若BC·BD=
(3)若BC·BD=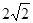 ,求正方形ABCD的面积.
,求正方形ABCD的面积.
【答案】
(1)因为四边形ABCD是正方形,所以BC=DC, ∠DCB=∠
DCF=90°,而CF=CE,则△BCE≌△DCF.
(2)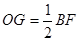
由(1)知△BCE≌△DCF,所以∠CDF=∠CBE,且∠CEB=∠
DEG,则∠DGE=∠BCE=90°,又因为BE平分∠DBC,所以GF=GD.而O正方形ABCD的中心,则OG是△DBF的中位线,所以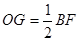 .
.
(3)因为四边形ABCD是正方形,所以BC=DC,且∠DCB=90°.在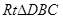 中有
中有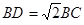 ,又因为
,又因为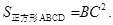 BC·BD=
BC·BD=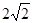 ,所以
,所以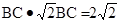
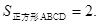
【解析】略

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.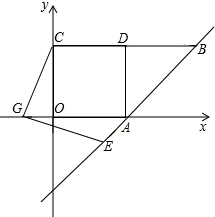
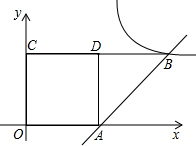



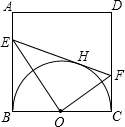 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.