题目内容
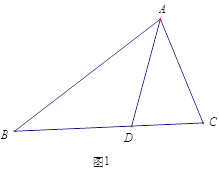
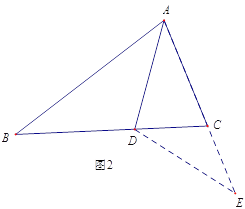
【题目】如图，△ABC是⊙O的内接三角形，∠BAD是△ABC的一个外角，∠BAC、∠BAD的平分线分别交⊙O于点E、F．请你在图上连接EF．（1）证明：EF是⊙O的直径；（2）请你判断EF与BC有怎样的位置关系？并请证明你的结论．
【答案】 (1)详见解析；（2）EF垂直平分BC，证明详见解析.
【解析】
（1）先利用角平分线定义和平角定义计算出∠EAF=90°，则利用圆周角定理的推论得到EF为⊙O的直径；
（2）由AE平分∠BAC得∠BAE=∠CAE，根据圆周角定理得
=
，于是根据垂径定理的推论可得EF垂直平分BC．
（1）连接EF．
∵AF平分∠BAD，AE平分∠BAC，∴∠BAF=
∠BAD，∠BAE=∠BAC，∴∠BAF+∠BAE=（∠BAD+∠BAC）=×180°=90°，即∠EAF=90°，∴EF为⊙O的直径．
（2）EF垂直平分BC．理由如下：
∵AE平分∠BAC，∴∠BAE=∠CAE，∴=．
∵EF为⊙O的直径，∴EF垂直平分BC．
练习册系列答案
期末集结号系列答案
相关题目
