题目内容
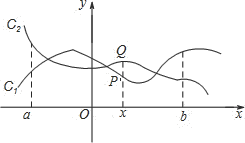
【题目】如图,点![]() 与
与![]() 分别是两个函数图象
分别是两个函数图象![]() 与
与![]() 上的任一点.当
上的任一点.当![]() 时,有
时,有![]() 成立,则称这两个函数在
成立,则称这两个函数在![]() 上是“相邻函数”,否则称它们在
上是“相邻函数”,否则称它们在![]() 上是“非相邻函数”.例如,点
上是“非相邻函数”.例如,点![]() 与
与![]() 分别是两个函数
分别是两个函数![]() 与
与![]() 图象上的任一点,当
图象上的任一点,当![]() 时,
时, ![]() ,通过构造函数
,通过构造函数![]() 并研究它在
并研究它在![]() 上的性质,得到该函数值得范围是
上的性质,得到该函数值得范围是![]() ,所以
,所以![]() 成立,因此这两个函数在
成立,因此这两个函数在![]() 上是“相邻函数”.
上是“相邻函数”.
(![]() )判断函数
)判断函数![]() 与
与![]() 在
在![]() 上是否为“相邻函数”,并说明理由.
上是否为“相邻函数”,并说明理由.
(![]() )若函数
)若函数![]() 与
与![]() 在
在![]() 上是“相邻函数”,求
上是“相邻函数”,求![]() 的取值范围.
的取值范围.
(![]() )若函数
)若函数![]() 与
与![]() 在
在![]() 上是“相邻函数”,直接写出
上是“相邻函数”,直接写出![]() 的最大值与最小值.
的最大值与最小值.
【答案】(1)见解析(2)![]() ;(3)
;(3)![]() 的最大值为
的最大值为![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
【解析】(1)直接利用相邻函数的定义结合一次函数增减性,得出当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1,进而判断即可;
(2)直接利用相邻函数的定义结合二次函数增减性,得出当x=1时,函数有最大值a-1,当x=0,或x=2时,函数有最大值a,即a-1≤y≤a,进而判断即可;
(3)直接利用相邻函数的定义结合函数增减性,得出当x=1时,函数有最大值a-2,当x=2时,函数有最大值![]() ,即a-2≤y≤
,即a-2≤y≤![]() ,进而判断即可.
,进而判断即可.
解:(![]() )函数
)函数![]() 与
与![]() ,在
,在![]() 上为“相邻函数”.
上为“相邻函数”.
∵![]() ,
,
∴为相邻函数.
(![]() )
)![]()
![]()
![]() .
.
∴![]() .
.
①当![]() ,即
,即![]() 时.
时.
![]() ,
,
∴![]() 无解.
无解.
②![]() ,即
,即![]() 时,
时,
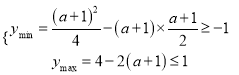
∴![]() .
.
③![]() 即
即![]() 时.
时.
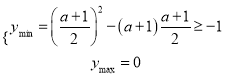 .
.
∴![]() 无解.
无解.
④当![]() 即
即![]() 时.
时.
![]() ,
,
∴![]() ,无解.
,无解.
综上所得: ![]() .
.
(![]() )∵当
)∵当![]() 时
时![]() .
.
![]() 时,
时, ![]() .
.
∴![]() ,
,
∴![]() .
.
当![]() 时
时![]() ,
,
![]() 时
时![]() .
.
∴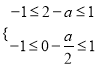 ,
,
∴![]() .
.
综上所得: ![]() 与
与![]() 在
在![]() 上,
上,
是“相邻函数”时.
![]() 的最大值为
的最大值为![]() .
.
![]() 的最小值为
的最小值为![]() .
.
“点睛”此题主要考查了函数的综合以及函数增减性和新定义,根据题意正确理解“相邻函数”的定义是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目



