题目内容
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.
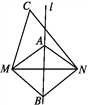
∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
【答案】D
【解析】解:根据题意,第一个空,由垂直平分线得到线段相等,应用了性质,填①;
第二个空,由线段相等得点在直线上,应用了判定,填②;
应用了垂直平分线的性质,填①.
应所以填①②①,故选D.

练习册系列答案
相关题目