题目内容
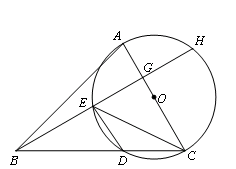
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
小题1:求证:△ABD∽△AEB;
小题2:若AD=1,DE=3,求⊙O半径的长.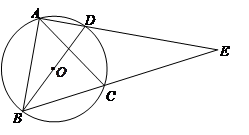
小题1:求证:△ABD∽△AEB;
小题2:若AD=1,DE=3,求⊙O半径的长.
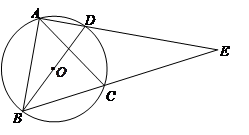
小题1:见解析。
小题2:
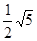
解:(1)证明:∵AB=AC,∴弧AB=弧AC. ∴∠ABC=∠ADB.……………1分
又∠BAE=∠DAB,∴△ABD∽△AEB. ………………………………… 3分
(2)解:∵△ABD∽△AEB, ∴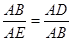 .
.
∵ AD=1,DE=3, ∴AE=4. ∴ AB2=AD·AE=1×4=4.
∴ AB=2. ……………………………………………………………………6分
∵ BD是⊙O的直径, ∴∠DAB=90°.
在Rt△ABD中,BD2=AB2+AD2=22+12=5,
∴BD=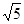 .∴⊙O的半径为
.∴⊙O的半径为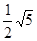
又∠BAE=∠DAB,∴△ABD∽△AEB. ………………………………… 3分
(2)解:∵△ABD∽△AEB, ∴
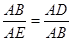 .
.∵ AD=1,DE=3, ∴AE=4. ∴ AB2=AD·AE=1×4=4.
∴ AB=2. ……………………………………………………………………6分
∵ BD是⊙O的直径, ∴∠DAB=90°.
在Rt△ABD中,BD2=AB2+AD2=22+12=5,
∴BD=
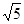 .∴⊙O的半径为
.∴⊙O的半径为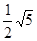

练习册系列答案
相关题目


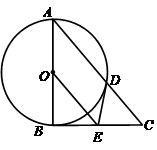
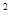 =2CD·OE;
=2CD·OE;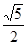 ,DE=2,求AD的长
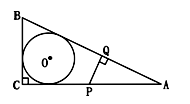
,DE=2,求AD的长 C=90°,AC=4,BC=3,以△ABC的一边为边作等腰三角形,使它的第三个顶点在△ABC的其他边上.请在图①、图②、图③中分别画出一个符合条件得等腰三角形,且三个图形中的等腰三角形各不相同,并在图中标明所画等腰三角形的腰长(不要求尺规作图). (6分)
C=90°,AC=4,BC=3,以△ABC的一边为边作等腰三角形,使它的第三个顶点在△ABC的其他边上.请在图①、图②、图③中分别画出一个符合条件得等腰三角形,且三个图形中的等腰三角形各不相同,并在图中标明所画等腰三角形的腰长(不要求尺规作图). (6分)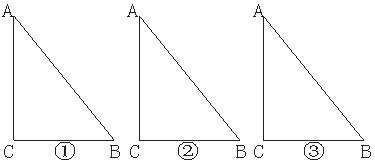


 △
△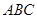 中,∠
中,∠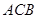 =90°,
=90°,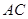 =4,
=4,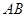 =5,点
=5,点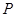 是
是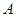 、点
、点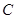 重合),PQ⊥
重合),PQ⊥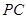 的值为( ▲ )
的值为( ▲ )