题目内容
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
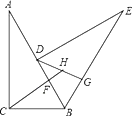
【答案】(1)SAS全等(2)120°
【解析】试题分析:(1)在△CBF和△DBG中,根据SAS即可证得两个三角形全等,根据全等三角形的对应边相等即可证得;
(2)根据全等三角形的对应角相等,即可证得∠DHF=∠CBF=60°,从而求解.
试题解析:(1)证明:∵在△CBF和△DBG中,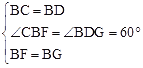 ,
,
∴△CBF≌△DBG(SAS).
∴CF=DG.
(2)∵△CBF≌△DBG,∴∠BCF=∠BDG.
又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°.
∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.

练习册系列答案
相关题目