题目内容
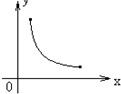
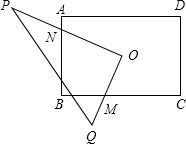 如图,O为矩形ABCD的中心,将直角△OPQ的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是
如图,O为矩形ABCD的中心,将直角△OPQ的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是
- A.
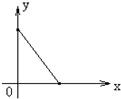
- B.
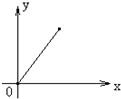
- C.
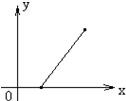
- D.
C
分析:过点O分别作OF⊥AB与F,OE⊥BC与E,易证明△NOF∽△MOE,利用相似比作为相等关系即可得到关于x,y的方程,整理即可得到函数关系式从而判断图象.
解答: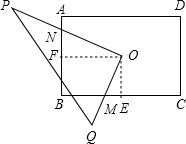 解:过点O分别作OF⊥AB与F,OE⊥BC与E
解:过点O分别作OF⊥AB与F,OE⊥BC与E
∵∠POQ=∠EOF=90°
∴∠NOF=∠MOE
∵∠NFO=∠MEO=90°
∴△NOF∽△MOE
∴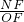 =
=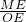
∵AB=4,AD=6,BM=x,AN=y
∴NF=2-y,ME=3-x,OF=3,OE=2
∴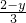 =
=
∴y= x-
x- (0<x<6)
(0<x<6)
故选C.
点评:解决有关动点问题的函数图象类习题时,关键是要根据条件找到所给的两个变量之间的函数关系,尤其是在几何问题中,更要注意基本性质的掌握和灵活运用.
分析:过点O分别作OF⊥AB与F,OE⊥BC与E,易证明△NOF∽△MOE,利用相似比作为相等关系即可得到关于x,y的方程,整理即可得到函数关系式从而判断图象.
解答:
 解:过点O分别作OF⊥AB与F,OE⊥BC与E
解:过点O分别作OF⊥AB与F,OE⊥BC与E∵∠POQ=∠EOF=90°
∴∠NOF=∠MOE
∵∠NFO=∠MEO=90°
∴△NOF∽△MOE
∴
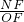 =
=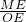
∵AB=4,AD=6,BM=x,AN=y
∴NF=2-y,ME=3-x,OF=3,OE=2
∴
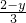 =
=
∴y=
 x-
x- (0<x<6)
(0<x<6)故选C.
点评:解决有关动点问题的函数图象类习题时,关键是要根据条件找到所给的两个变量之间的函数关系,尤其是在几何问题中,更要注意基本性质的掌握和灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.
26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.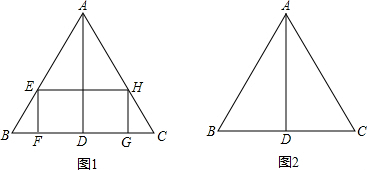


 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为