题目内容
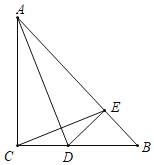
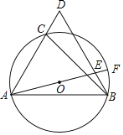
【题目】如图,点C是等边△ABD的边AD上的一点,且∠ACB=75°,⊙O是△ABC的外接圆,连结AO并延长交BD于E、交⊙O于F.
(1)求证:∠BAF=∠CBD;
(2)过点C作CG∥AE交BD于点G,求证:CG是⊙O的切线;
(3)在(2)的条件下,当AF=2![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)2﹣![]() .
.
【解析】
(1)利用已知条件分别求出∠BAF=15°,∠CBD=15°,即可证明∠BAF=∠CBD;
(2)过点C作CG∥AE交BD于点G,连接CO,∠CAF=∠CAB﹣∠BAF=60°﹣15°=45°,∠ACF=90°,所以∠CFA=45°,CA=CF,CO⊥AF,由CG∥AE,所以CO⊥CG,因此CG是⊙O的切线;
(3)证明△DCG∽△ABC,然后利用相似比求![]() 的值.
的值.
解:(1)如图,连接CF.
∵AF为直径,
∴∠ACF=90°,
∵∠ACB=75°,
∴∠BCF=90°﹣75°=15°,
∴∠BAF=15°,
∵△ABD为等边三角形,
∴∠D=∠DAB=∠DBA=60°,
∴∠CBD=∠ACB﹣∠D=75°﹣60°=15°,
∴∠BAF=∠CBD;
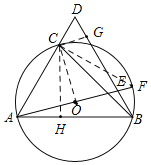
(2)过点C作CG∥AE交BD于点G,连接CO,
∵∠CAF=∠CAB﹣∠BAF=60°﹣15°=45°,
∠ACF=90°,
∴∠CFA=45°,
∴CA=CF,
∴CO⊥AF,
∵CG∥AE,
∴CO⊥CG,
∴CG是⊙O的切线;
(3)作CH⊥AB于H,
∵AF=![]() ,
,
∴AC=CF=![]() AF=2,
AF=2,
在△ACB中,
∠CAB=60°,∠ACB=75°,∠ABC=45°,
∴∠ACH=30°,∠HCB=∠HBC=45°,
∴AH=![]() AC=1,CH=
AC=1,CH=![]() ,AH=
,AH=![]() ,BH=CH=
,BH=CH=![]() ,
,
∴AB=AH+BH=1+![]() ,
,
∴AD=AB=![]() ,CD=AD﹣AC=
,CD=AD﹣AC=![]()
∵CG∥AE,
∴∠DCG=∠CAF=45°,
在△DCG与△ABC中,
∠DCG=∠ABC=45°,∠D=∠CAB=60°,
∴△DCG∽△ABC,
∴![]() ,
,
∴![]() 的值为
的值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案