题目内容
（2013•嘉定区二模）已知AP是半圆O的直径，点C是半圆O上的一个动点（不与点A、P重合），联结AC，以直线AC为对称轴翻折AO，将点O的对称点记为O1，射线AO1交半圆O于点B，联结OC．
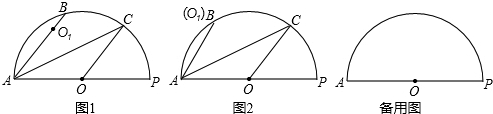
（1）如图1，求证：AB∥OC；
（2）如图2，当点B与点O1重合时，求证：
=
；
（3）过点C作射线AO1的垂线，垂足为E，联结OE交AC于F．当AO=5，O1B=1时，求
的值．
（1）如图1，求证：AB∥OC；
（2）如图2，当点B与点O1重合时，求证：
 |
| AB |
|
| CB |
（3）过点C作射线AO1的垂线，垂足为E，联结OE交AC于F．当AO=5，O1B=1时，求
| CF |
| AF |
分析：（1）利用对称性得出∠OAC=∠O1AC，再利用等边对等角得出∠OAC=∠C，即可得出∠C=∠O1AC，求出AB∥OC即可；
（2）由点O1与点O关于直线AC对称，AC⊥OO1，由点O1与点B重合，可得AC⊥OB，再利用垂径定理推论得出AB=CB；
（3）分别根据当点O1在线段AB上以及当点O1在线段AB的延长线上时分别求出AE的长即可得出答案．
（2）由点O1与点O关于直线AC对称，AC⊥OO1，由点O1与点B重合，可得AC⊥OB，再利用垂径定理推论得出AB=CB；
（3）分别根据当点O1在线段AB上以及当点O1在线段AB的延长线上时分别求出AE的长即可得出答案．
解答：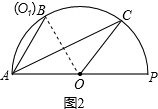
解：（1）∵点O1与点O关于直线AC对称，
∴∠OAC=∠O1AC．
在⊙O中，
∵OA=OC，
∴∠OAC=∠C．
∴∠C=∠O1AC，
∴O1A∥OC，
即AB∥OC；
（2）方法一：如图2，连结OB．
∵点O1与点O关于直线AC对称，AC⊥OO1，
由点O1与点B重合，可得AC⊥OB．
∵点O是圆心，AC⊥OB，
∴AB=CB，
方法2：∵点O1与点O关于直线AC对称，
∴AO=AO1，CO=CO1，
由点O1与点B重合，可得 AO=AB，CB=CO，
∵OA=OC，
∴AB=CB．
∴AB=CB，
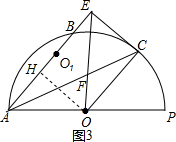
（3）当点O1在线段AB上（如图3），过点O作OH⊥AB，垂足为H．
∵OH⊥AB，CE⊥AB，
∴OH∥CE，
又∵AB∥OC，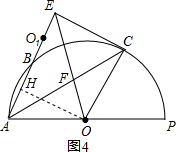
∴HE=OC=5．
∵AB=AO1+O1B=AO+O1B=6，
又∵OH⊥AB，
∴AH=
AB=3．
∴AE=EH+AH=5+3=8，
∵AB∥OC，
∴
=
=
，
当点O1在线段AB的延长线上，如图4，
过点O作OH⊥AB，垂足为H．
∵OH⊥AB，CE⊥AB，
∴OH∥CE，
又∵AB∥OC，
∴HE=OC=5．
∵AB=AO1-O1B=AO-O1B=4，
又∵OH⊥AB，
∴AH=
AB=2．
∴AE=EH+AH=5+2=7，
∵AB∥OC，
∴
=
=
．
解：（1）∵点O1与点O关于直线AC对称，∴∠OAC=∠O1AC．
在⊙O中，
∵OA=OC，
∴∠OAC=∠C．
∴∠C=∠O1AC，
∴O1A∥OC，
即AB∥OC；
（2）方法一：如图2，连结OB．
∵点O1与点O关于直线AC对称，AC⊥OO1，
由点O1与点B重合，可得AC⊥OB．
∵点O是圆心，AC⊥OB，
∴AB=CB，
方法2：∵点O1与点O关于直线AC对称，
∴AO=AO1，CO=CO1，
由点O1与点B重合，可得 AO=AB，CB=CO，
∵OA=OC，
∴AB=CB．
∴AB=CB，
（3）当点O1在线段AB上（如图3），过点O作OH⊥AB，垂足为H．
∵OH⊥AB，CE⊥AB，
∴OH∥CE，
又∵AB∥OC，
∴HE=OC=5．
∵AB=AO1+O1B=AO+O1B=6，
又∵OH⊥AB，
∴AH=
| 1 |
| 2 |
∴AE=EH+AH=5+3=8，
∵AB∥OC，
∴
| CF |
| AF |
| OC |
| AE |
| 5 |
| 8 |
当点O1在线段AB的延长线上，如图4，
过点O作OH⊥AB，垂足为H．
∵OH⊥AB，CE⊥AB，
∴OH∥CE，
又∵AB∥OC，
∴HE=OC=5．
∵AB=AO1-O1B=AO-O1B=4，
又∵OH⊥AB，
∴AH=
| 1 |
| 2 |
∴AE=EH+AH=5+2=7，
∵AB∥OC，
∴
| CF |
| AF |
| CO |
| AE |
| 5 |
| 7 |
点评：此题主要考查了圆的综合应用以及垂径定理和关于直线对称的性质等知识，利用数形结合以及分类讨论的思想得出是解题关键．
练习册系列答案
相关题目
（2013•嘉定区二模）如图，点E是正方形ABCD边BC上的一点（不与B、C重合），点F在CD边的延长线上，且满足DF=BE．联结EF，点M、N分别是EF与AC、AD的交点．
（2013•嘉定区二模）已知平面直角坐标系xOy（如图），抛物线