题目内容
 (2013•嘉定区二模)已知平面直角坐标系xOy(如图),抛物线y=
(2013•嘉定区二模)已知平面直角坐标系xOy(如图),抛物线y=| 1 |
| 2 |
| 3 |
| 2 |
(1)求该抛物线顶点P的坐标;
(2)求tan∠CAP的值;
(3)设Q是(1)中所求出的抛物线的一个动点,点Q的横坐标为t,当点Q在第四象限时,用含t的代数式表示△QAC的面积.
分析:(1)将已知点的坐标代入到给定的函数的解析式中求解即可;
(2)延长AP交y轴于G,过C作CH⊥AG,垂足是H,首先求得直线AP的解析式,然后表示出有关线段长,从而求得tan∠CAP的值;
(3)利用 S△QAC=S△AOC+S△QOC-S△AOQ求解即可.
(2)延长AP交y轴于G,过C作CH⊥AG,垂足是H,首先求得直线AP的解析式,然后表示出有关线段长,从而求得tan∠CAP的值;
(3)利用 S△QAC=S△AOC+S△QOC-S△AOQ求解即可.
解答:解:(1)将A(-3,0)、C(0,-
).代入y=
x2+bx+c得
解得
所以抛物线的表达式为y=
x2+x-
.
其顶点P的坐标为(-1,-2).…(1分)
(2)延长AP交y轴于G,过C作CH⊥AG,垂足是H.
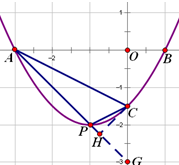 设直线AP的表达式为y=kx+b,
设直线AP的表达式为y=kx+b,
将A(-3,0)、P(1,-2)代入,得
,解得
.
∴y=-x-3.
进而可得G(0,-3).
∴OG=OA,∠G=∠OAG=45°,
在Rt△CHG中,HG=CH=CG•sin45°=
.
在Rt△AOG中,AG=
=3
,
∴AH=AG-HG=
∴tan∠CAP=
=
.
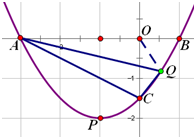
(3)设Q(t,
t2+t-
),
由Q在第四象限,得|t|=t,|
t2+t-
|=-
t2-t+
).
联结OQ,易得 S△QAC=S△AOC+S△QOC-S△AOQ.
∵S△AOC=
×|-3|×|-
|=
,S△QOC=
×|-
|×t=
t,
S△AOQ=
×|-3|×|
t2+t-
|=-
t2-
t+
,
∴S△QAC=
+
t-(-
t2-
t+
)=
t2+
t.
| 3 |
| 2 |
| 1 |
| 2 |
|
|
所以抛物线的表达式为y=
| 1 |
| 2 |
| 3 |
| 2 |
其顶点P的坐标为(-1,-2).…(1分)
(2)延长AP交y轴于G,过C作CH⊥AG,垂足是H.
 设直线AP的表达式为y=kx+b,
设直线AP的表达式为y=kx+b,将A(-3,0)、P(1,-2)代入,得
|
|
∴y=-x-3.
进而可得G(0,-3).
∴OG=OA,∠G=∠OAG=45°,
在Rt△CHG中,HG=CH=CG•sin45°=
3
| ||
| 4 |
在Rt△AOG中,AG=
| OG |
| cos45° |
| 2 |
∴AH=AG-HG=
9
| ||
| 4 |

∴tan∠CAP=
| CH |
| AH |
| 1 |
| 3 |
(3)设Q(t,
| 1 |
| 2 |
| 3 |
| 2 |
由Q在第四象限,得|t|=t,|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
联结OQ,易得 S△QAC=S△AOC+S△QOC-S△AOQ.
∵S△AOC=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
S△AOQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
∴S△QAC=
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
点评:此题主要考查了二次函数的综合题目,利用一般式求二次函数解析式及解直角三角形是考查的重点内容,同学们应学会应用.

练习册系列答案
相关题目
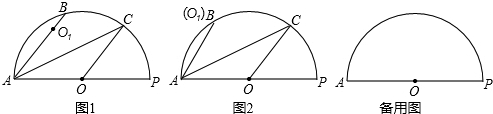

 (2013•嘉定区二模)如图,点E是正方形ABCD边BC上的一点(不与B、C重合),点F在CD边的延长线上,且满足DF=BE.联结EF,点M、N分别是EF与AC、AD的交点.
(2013•嘉定区二模)如图,点E是正方形ABCD边BC上的一点(不与B、C重合),点F在CD边的延长线上,且满足DF=BE.联结EF,点M、N分别是EF与AC、AD的交点.