题目内容
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC=2,BD平分∠ABC,∠A=60°.求:梯形ABCD的周长. 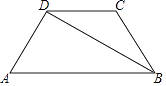
【答案】解:在梯形ABCD中,∵DC∥AB,AD=BC=2,∠A=60°. ∴∠ABC=∠A=60°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∴∠ADB=90°,
∴AD= ![]() AB.
AB.
∴AB=2AD=4.
又 DC∥AB,
∴∠CDB=∠ABD,
又∠ABD=∠CBD,
∴∠CDB=∠CBD.
∴CD=BC=2.
∴梯形ABCD的周长=AB+BC+CD+AD=4+2+2+2=10
【解析】由等腰梯形的性质得出∴∠ABC=∠A=60°.周长∠ABD=∠CBD=30°,∠ADB=90°,由直角三角形的性质得出AD= ![]() AB.AB=2AD=4.证出∠CDB=∠CBD.得出CD=BC=2.即可求出梯形ABCD的周长.
AB.AB=2AD=4.证出∠CDB=∠CBD.得出CD=BC=2.即可求出梯形ABCD的周长.
【考点精析】解答此题的关键在于理解梯形的定义的相关知识,掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目