��Ŀ����
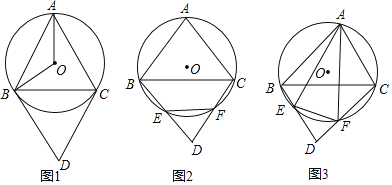
����Ŀ��B��C����O�ϵ��������㣬A��Բ�ϵĶ��㣬0������BAC��90����BD��AC��CD��AB��
��1����ͼ1�������ABC�ǵȱ������Σ���֤BD����O�����ߣ�
��2����ͼ2�����60������BAC��90����BD��CD�ֱ���O��E��F���о������ABEFC�����ʣ�
��̽��AE��AF��BC��������ϵ����֤����Ľ��ۣ�
����ͼ3������O�İ뾶Ϊ4����BAC��75�������EF�ij���
����AB��c��AC��b��ֱ��д��BE��CF��������ϵ��
���𰸡���1������������2����AE��BC��AF��BC�����ɼ���������EF��4����![]() ��
��![]() ��
��
��������
��1����취֤��OB��BD���ɽ�����⣮
��2���ٽ��ۣ�AE��BC��AF��BC����취֤����AB=��EC,��AE=��BC���ɽ�����⣮
����ͼ3�У�����OE��OF��EC��BF��֤����OEF�ǵȱ������μ��ɽ�����⣮
���������������ε����ʽ�����⼴�ɣ�
�⣺��1����ͼ1�У�
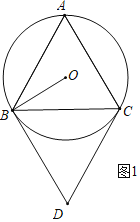
��BD��AC��CD��AB��
���ı���ABDC��ƽ���ı��Σ�
��AB��CD��BD��AC��
�ߡ�ABC�ǵȱ������Σ�
��AB��BC��AC��
��BC��BD��CD��
���BCD�ǵȱ������Σ�
���CBD��60����
�ߵ�O�ǵȱ���ABC�����ģ�
���OCB��30����
���OBD��90����
��OB��BD��
��BD�ǡ�O�����ߣ�
��2���ٽ��ۣ�AE��BC��AF��BC��
���ɣ���ͼ2�У�����BF��EC��
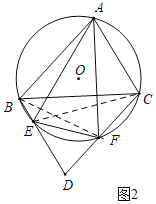
��BD��AC��
���ACB����CBE��
�AB=��EC,
�AE=��BC��
��AE��BC��ͬ����֤��AF��BC��
����ͼ3�У�����OE��OF��EC��BF��
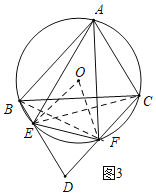
�ɢٿ�֪AE��AF��
���AEF����AFE��
��AE=��BC��
���ACE����BAC��75����
���AFE����ACE��75����
���AEF����AFE��75����
���EAF��180����75����75����30����
���EOF��2��EAF��60����
��OE��OF��
���OEF�ǵȱ������Σ�
��EF��OE��4��
�۽��ۣ�![]() ��
��
���ɣ���ͼ3�У��ߡ�EFD+��EFC=180������EFC+��DBC=180����
���EFD=��DBC��
���DFE�ס�DBC��
���DFE�ס�DBC��
��![]() ��
��
���ı���ABDC��ƽ���ı��Σ�
��AB=CD=c��BD=AC=b��
��![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�