题目内容
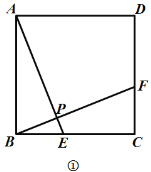
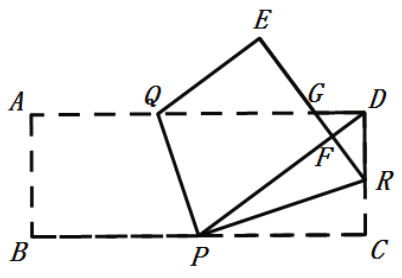
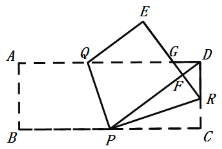
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 在
在![]() 上,连接
上,连接![]() ,折叠矩形,点
,折叠矩形,点![]() 与点
与点![]() 都恰好落在
都恰好落在![]() 上的点
上的点![]() 处,折痕是
处,折痕是![]() 、
、![]() 、
、![]() 的对应线段
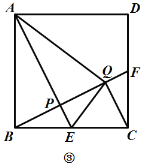
的对应线段![]() 与
与![]() 交于点
交于点![]() ,则线段
,则线段![]() 的长度是______.
的长度是______.
【答案】![]() ;
;
【解析】
根据折叠的性得到PC=PF =4,FR=RC,在Rt△PDC中,求得PD、DF的长,在Rt△DFR中,求得![]() ,证得Rt△DFR
,证得Rt△DFR![]() Rt△GFD,求得
Rt△GFD,求得![]() ,再证得Rt△EGQ
,再证得Rt△EGQ![]() Rt△FGD,即可求解.
Rt△FGD,即可求解.
∵折叠矩形,点![]() 与点
与点![]() 都恰好落在
都恰好落在![]() 上的点
上的点![]() 处,
处,
∴PC=PF=PB,
∵矩形![]() 中,
中,![]() ,
,![]() ,
,
∴BC=AD=8,AB=CD=3,
∴PC=PF=![]() BC=4,
BC=4,
在Rt△PDC中,PD=![]() ,
,
∴DF=PD-PF=5-4=1,
根据折叠的性质,△PCR![]() △PFR,
△PFR,
∴RC=FR,∠C=∠PFR=90![]() ,
,
在Rt△DFR中,DF=1,DR=CD-RC=3-FR,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
在Rt△FDR和Rt△FGD中,
∠FDR+∠FDG=90![]() ,∠FGD+∠FDG=90
,∠FGD+∠FDG=90![]() ,
,
∴∠FDR=∠FGD,
∴Rt△DFR![]() Rt△GFD,
Rt△GFD,
∴![]() ,即
,即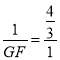 ,
,
∴![]() ,
,
∴DG=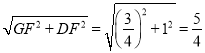 ,
,
根据折叠的性质,EF=AB=3,∠E=∠B=90![]() ,
,
∴EG=EF-GF=3-![]() ,
,
∵∠E=∠DFG=90![]() ,∠EGQ=∠FGD,
,∠EGQ=∠FGD,
∴Rt△EGQ![]() Rt△FGD,
Rt△FGD,
∴![]() ,即
,即 ,
,
∴QG=![]() (
(![]() ) .
) .
故答案为:![]() .
.

练习册系列答案
相关题目