题目内容
 如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:
如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:(1)过点A、B、C的二次函数关系式;
(2)求△ABE面积的最大值.
分析:(1)先根据∠AOB=90°,∠BAO=30°,且A的坐标为(3,0)求出B点坐标,用待定系数法求出过点A、B、C的二次函数关系式即可;
(2)由题意可得当⊙C与AD相切时,△ABE面积最大,然后连接CD,由切线的性质,根据勾股定理,可求得AD的长,易证得△AOE∽△ADC,根据相似三角形的对应边成比例,易求得OE的长,继而求得△ABE面积的最大值.
(2)由题意可得当⊙C与AD相切时,△ABE面积最大,然后连接CD,由切线的性质,根据勾股定理,可求得AD的长,易证得△AOE∽△ADC,根据相似三角形的对应边成比例,易求得OE的长,继而求得△ABE面积的最大值.
解答: 解:(1)∵Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),
解:(1)∵Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),
∴B(0,
),
设过A、B、C三点的函数关系式为y=a(x+1)(x-3),把点B(0,
)代入得,
∴
=a×1×(-3),解得a=-
,
∴过点A、B、C的二次函数关系式为:y=-
(x+1)(x-3),即y=-
x2+
x+
;
(2)∵△ABE的高OA是定值,
∴BE越长,则△ABE的面积越大,
∴当⊙C与AD相切时,△ABE面积最大,连接CD,
则∠CDA=90°,
∵A(3,0),B(0,
),⊙C的圆心为点C(-1,0),半径为1,
∴CD=1,AC=3+1=4,
∴AD=
=
=
,
∵∠AOE=∠ADC=90°,∠EAO=∠CAD,
∴△AOE∽△ADC,
∴
=
,
=
,解得OE=
,
∴BE=OB+OE=
+
,
∴S△ABE最大=
BE•OA=
×(
+
)×3=
+
.
 解:(1)∵Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),
解:(1)∵Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),∴B(0,
| 3 |
设过A、B、C三点的函数关系式为y=a(x+1)(x-3),把点B(0,
| 3 |
∴
| 3 |
| ||
| 3 |
∴过点A、B、C的二次函数关系式为:y=-
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)∵△ABE的高OA是定值,
∴BE越长,则△ABE的面积越大,
∴当⊙C与AD相切时,△ABE面积最大,连接CD,
则∠CDA=90°,
∵A(3,0),B(0,
| 3 |
∴CD=1,AC=3+1=4,
∴AD=
| AC2-CD2 |
| 42-12 |
| 15 |
∵∠AOE=∠ADC=90°,∠EAO=∠CAD,
∴△AOE∽△ADC,
∴
| OA |
| AD |
| OE |
| CD |
| 3 | ||
|
| OE |
| 1 |
| ||
| 5 |
∴BE=OB+OE=
| 3 |
| ||
| 5 |
∴S△ABE最大=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 5 |
3
| ||
| 2 |
3
| ||
| 10 |
点评:本题考查的是二次函数综合题,涉及到切线的性质、相似三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,已知Rt△ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于D点,连接AO、HE、HF,则下列结论:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )
如图,已知Rt△ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于D点,连接AO、HE、HF,则下列结论:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )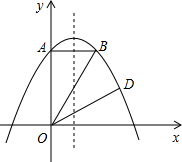 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由. 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由. ,
, ).
). ,
, ).
).
