题目内容
(2009•新洲区模拟)如图,已知Rt△ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于D点,连接AO、HE、HF,则下列结论:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
【答案】分析:连接OE,OH,OF,OB,
①由切线的性质和四边形的内角和即可判定;
②同①的方法得∠FOH=180°-∠C=90°+∠BAC,再圆周角定理即可得到证明结论正确;
③根据已知条件知道四边形OEBH是正方形,然后证明△BDE≌△FAO,然后即可题目结论;
④根据已知条件可以证明△DFH∽△ABO,根据相似三角形的对应边成比例和已知条件即可证明结论正确.
解答: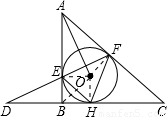 解:①中,连接OE,OH,
解:①中,连接OE,OH,
则OE⊥AB,OH⊥BC,
∴∠EOH=90°,
∴∠EFH= ∠EOH=45°,正确;
∠EOH=45°,正确;
②中,同①的方法得∠FOH=180°-∠C=90°+∠BAC,
根据圆周角定理得∠FEH= ∠FOH=45°+∠FAO,正确;
∠FOH=45°+∠FAO,正确;
③中,连接OF,由①得四边形OEBH是正方形,则圆的半径=BE,
即OF=BE,
又∵∠DBE=∠AFO,∠BED=∠AEF=∠AFE,
则△BDE∽△FAO,
得BD=AF,正确;
④中,连接OB,根据两个角对应相等得△DFH∽△ABO,则DH•AB=AO•DF,又∵AB=DH,所以结论正确.
故选D.
点评:此题综合运用了切线的性质定理、切线长定理、圆周角定理和相似三角形的性质和判定,综合性比较强.
①由切线的性质和四边形的内角和即可判定;
②同①的方法得∠FOH=180°-∠C=90°+∠BAC,再圆周角定理即可得到证明结论正确;
③根据已知条件知道四边形OEBH是正方形,然后证明△BDE≌△FAO,然后即可题目结论;
④根据已知条件可以证明△DFH∽△ABO,根据相似三角形的对应边成比例和已知条件即可证明结论正确.
解答:
 解:①中,连接OE,OH,
解:①中,连接OE,OH,则OE⊥AB,OH⊥BC,
∴∠EOH=90°,
∴∠EFH=
 ∠EOH=45°,正确;
∠EOH=45°,正确;②中,同①的方法得∠FOH=180°-∠C=90°+∠BAC,
根据圆周角定理得∠FEH=
 ∠FOH=45°+∠FAO,正确;
∠FOH=45°+∠FAO,正确;③中,连接OF,由①得四边形OEBH是正方形,则圆的半径=BE,
即OF=BE,
又∵∠DBE=∠AFO,∠BED=∠AEF=∠AFE,
则△BDE∽△FAO,
得BD=AF,正确;
④中,连接OB,根据两个角对应相等得△DFH∽△ABO,则DH•AB=AO•DF,又∵AB=DH,所以结论正确.
故选D.
点评:此题综合运用了切线的性质定理、切线长定理、圆周角定理和相似三角形的性质和判定,综合性比较强.

练习册系列答案
相关题目
(2009•新洲区模拟)某公司现有甲、乙两种品牌的饮水机,其中甲品牌有A、B两种型号,乙品牌有C、D、E三种型号,各种型号饮水机的价格如下表:
某校计划从甲、乙两种品牌中各选购一种型号的饮水机.
(1)若各种型号的饮水机被选购的可能性相同,那么E型号饮水机被选购的概率是多少(要求利用列表法或树形图).
(2)某校购买了两种品牌的饮水机共30台,其中乙品牌只选购了E型号,共用去资金5000元,问E型号的饮水机买了多少台?
| 甲品牌 | 乙品牌 | ||||
| 型号 | A | B | C | D | E |
| 价格(元) | 200 | 170 | 130 | 120 | 100 |
(1)若各种型号的饮水机被选购的可能性相同,那么E型号饮水机被选购的概率是多少(要求利用列表法或树形图).
(2)某校购买了两种品牌的饮水机共30台,其中乙品牌只选购了E型号,共用去资金5000元,问E型号的饮水机买了多少台?
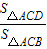 是否为一定值?若是定值,请求出其值;若不是定值,请说明理由.
是否为一定值?若是定值,请求出其值;若不是定值,请说明理由.


 的值.
的值.