Question

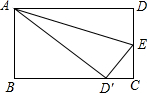
如图，直角三角形纸片ABC中，∠ACB=90°，AC=8，BC=6．折叠该纸片使点B与点C重合，折痕与AB、BC的交点分别为D、E．
（1）DE的长为______；
（2）将折叠后的图形沿直线AE剪开，原纸片被剪成三块，其中最小一块的面积等于______．

Answer 1

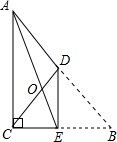
（1）根据题意得：DE⊥BC，CE=BE，
∵∠ACB=90°，
即AC⊥BC，
∴DE∥AC，
∴AD=BD，
∴DE=

1

2

AC=

1

2

×8=4；

（2）∵DE∥AC，DE=

1

2

AC，
∴△AOC∽△EOD，
∴OA：OE=AC：DE=2，
∵CE=

1

2

BC=

1

2

×6=3，
∵∠ACB=90°，AC=8，
∴S_△ACE=

1

2

CE•AC=

1

2

×3×8=12，
∴S_△OCE=

1

3

S_△ACE=4，
∴S_△ADE+S_△BDE=S_△ABC-4-12=8，
∴其中最小一块的面积等于4．
故答案为：（1）4，（2）4．