题目内容
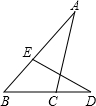
如图，AC⊥BD，AC=DC，BC=EC．求证：DE⊥AB．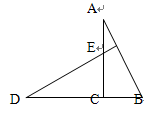
见解析
由已知求证Rt△ABC≌Rt△DCE，根据全等的性质知∠D=∠A，然后利用角的等量代换求得∠B+∠D=90º，从而求得结论
因为AC⊥BD，所以∠ACB=∠DCE=90º，所以∠A+∠B=90º．因为AC=DC，BC=EC，所以Rt△ABC≌Rt△DCE(HL)，所以∠D=∠A，所以∠B+∠D=90º，所以DE⊥AB．
因为AC⊥BD，所以∠ACB=∠DCE=90º，所以∠A+∠B=90º．因为AC=DC，BC=EC，所以Rt△ABC≌Rt△DCE(HL)，所以∠D=∠A，所以∠B+∠D=90º，所以DE⊥AB．
练习册系列答案
相关题目
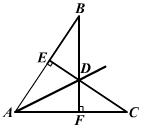
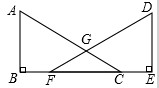
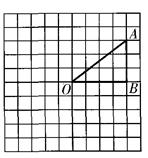
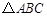的三边长a、b、c满足关系式
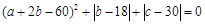，则