题目内容
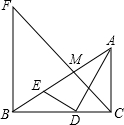 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F
(1)求证: .
.
(2)若BD=4,CD=3,求BE•AC的值.
(1)证明:连接DM.
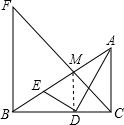 在Rt△ADE中,MD为斜边AE的中线,则DM=MA,
在Rt△ADE中,MD为斜边AE的中线,则DM=MA,
∴∠MDA=∠MAD,
∵AD平分∠BAC,
∴∠MAD=∠DAC,
∴∠MDA=∠DAC,
∴MD∥AC,
∵AC⊥BC,BF⊥BC,
∴BF∥AC,
∴DM∥BF∥AC,
∴ ,△ACM∽△BFM,
,△ACM∽△BFM,
∴ ,
,
∴ .
.
(2)解:∵∠AED=90°-∠EAD,∠ADC=90°-∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,
∴DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴BE•AC=BD•DC=4×3=12.
分析:(1)首先连接DM,由在Rt△ADE中,MD为斜边AE的中线,则DM=MA,又由AD平分∠BAC,易证得DM∥BF∥AC,可得 ,△ACM∽△BFM,继而证得
,△ACM∽△BFM,继而证得 .
.
(2)易证得△BED∽△BDA,△ADE∽△ACD,根据相似三角形的对应边成比例,即可得BE:BD=DC:AC,继而求得答案.
点评:此题考查了相似三角形的判定与性质、直角三角形的性质以及平行线分线段成比例定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
 在Rt△ADE中,MD为斜边AE的中线,则DM=MA,
在Rt△ADE中,MD为斜边AE的中线,则DM=MA,∴∠MDA=∠MAD,
∵AD平分∠BAC,
∴∠MAD=∠DAC,
∴∠MDA=∠DAC,
∴MD∥AC,
∵AC⊥BC,BF⊥BC,
∴BF∥AC,
∴DM∥BF∥AC,
∴
 ,△ACM∽△BFM,
,△ACM∽△BFM,∴
 ,
,∴
 .
.(2)解:∵∠AED=90°-∠EAD,∠ADC=90°-∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,
∴DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴BE•AC=BD•DC=4×3=12.
分析:(1)首先连接DM,由在Rt△ADE中,MD为斜边AE的中线,则DM=MA,又由AD平分∠BAC,易证得DM∥BF∥AC,可得
 ,△ACM∽△BFM,继而证得
,△ACM∽△BFM,继而证得 .
.(2)易证得△BED∽△BDA,△ADE∽△ACD,根据相似三角形的对应边成比例,即可得BE:BD=DC:AC,继而求得答案.
点评:此题考查了相似三角形的判定与性质、直角三角形的性质以及平行线分线段成比例定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

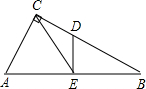 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=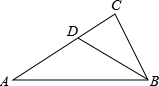 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )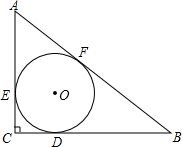 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.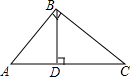 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.