题目内容
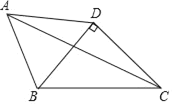
【题目】如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,求对角线AC的最大值.
,若对角线BD⊥CD于点D,求对角线AC的最大值.
【答案】AC最大值为![]() .
.
【解析】
以BC为边作等边△BCM(M点在BC下方),先证明△ABC≌△DBM,从而AC=DM,求DM最大值即可;以BC为直径作圆,当DM⊥BC时,DM最大.
解:以BC为边作等边△BCM(M点在BC下方),连接DM,
∵∠ABD=60°=∠CBM=60°,
∴∠ABC=∠DBM.
∵AB=DB,BC=BM,
∴△ABC≌△DBM(SAS).
∴AC=DM.
∴若求AC最大值,则求出DM最大值即可.
∵BC=![]() 是定值,∠BDC=90°,
是定值,∠BDC=90°,
∴点D在以BC为直径的圆上运动,如图所示.
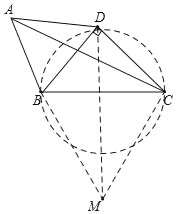
当D点在BC上方,DM⊥BC时,MD最大,此时最大值为![]() .
.
即AC最大值为![]() .
.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目