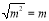题目内容
如图在Rt△ABC中,∠ACB=90°,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,求证: AC=EF
证明见解析
【解析】
试题分析:由∠ACB=90°,CD⊥AB可得∠ACD=∠B,再由ASA即可证得
试题解析:∵CD⊥AB ∠ACB=90°,
∴ ∠A+∠ACD=90o ∠A+∠B=90o
∴∠ACD=∠B
∵ EF⊥AC ,
∴∠CEF=∠ACB=90o
在△ABC与△FCE中
 ,
,
∴△ABC≌△FCE (ASA )
∴ AC=EF
考点:三角形全等的判定

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目