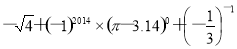题目内容
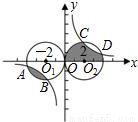
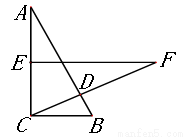
已知:如图所示,
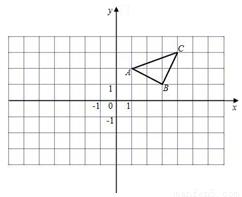
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
(1)作图见解析;A′(-1,2),B′(-3,1),C′(-4,3);
(2)画图见解析
【解析】
试题分析:(1)按要求作出图形,写出坐标即可
(2)找到点C关于x轴的对称点C”,然后连接AC”与x轴交点即为所求.
试题解析:(1)分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:A′(-1,2),
B′(-3,1),C′(-4,3).
(2)先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,(或找出A点关于x轴对称的点A″(1,-2),连接A″C交x轴于点P)则P点即为所求点.

考点:1、关于Y轴对称的图形;2、轴对称的应用;3、两点之间线段最短

练习册系列答案
相关题目
某校九年级一、二班学生参加同一次数学测验,经统计计算后得到下表:
班级 | 参加人数 | 中位数 | 方差 | 平均数 |
一班 | 55 | 78 | 135 | 75 |
二班 | 55 | 81 | 126 | 75 |
小亮根据上表分析得出如下结论:①一、二两班学生的平均水平相同;②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀);③一班成绩波动情况比二班成绩波动大.上述结论正确的是
A.①②③ B.①② C.①③ D.②③